题目内容
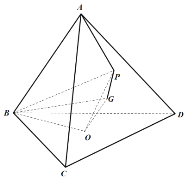
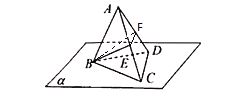
【题目】正四面体![]() 中,
中,![]() 在平面
在平面![]() 内,点
内,点![]() 是线段
是线段![]() 的中点,在该四面体绕
的中点,在该四面体绕![]() 旋转的过程中,直线
旋转的过程中,直线![]() 与平面
与平面![]() 所成角的余弦值不可能是( )
所成角的余弦值不可能是( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
【答案】A
【解析】
考虑相对运动,让四面体![]() 保持静止,平面
保持静止,平面![]() 绕着
绕着![]() 旋转,其垂线也绕着
旋转,其垂线也绕着![]() 旋转,取
旋转,取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() ,等价于平面
,等价于平面![]() 绕着
绕着![]() 旋转,推导出
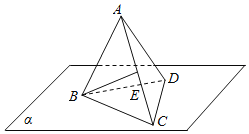
旋转,推导出![]() ,将问题抽象为几何模型,平面
,将问题抽象为几何模型,平面![]() 的垂线可视为圆锥的底面半径
的垂线可视为圆锥的底面半径![]() ,绕着圆锥的轴
,绕着圆锥的轴![]() 旋转,则
旋转,则![]() ,由此能求出结果.
,由此能求出结果.
解:考虑相对运动,让四面体![]() 保持静止,平面
保持静止,平面![]() 绕着
绕着![]() 旋转,
旋转,![]() 其垂线也绕着
其垂线也绕着![]() 旋转,如右图,取
旋转,如右图,取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() ,等价于平面
,等价于平面![]() 绕着
绕着![]() 旋转,设正四面体
旋转,设正四面体![]() 中棱长为2,在
中棱长为2,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
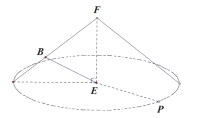
如下图示,将问题抽象为如下几何模型,平面![]() 的垂线可视为圆锥的底面半径
的垂线可视为圆锥的底面半径![]() ,绕着圆锥的轴
,绕着圆锥的轴![]() 旋转,显然
旋转,显然![]() ,则
,则![]() ,设
,设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则可得
,则可得![]() .
.
故选:A

练习册系列答案
相关题目