题目内容
设函数f(x)=|2x+1|-|x-4|.(1)解不等式f(x)＞2;
(2)若x∈［-1,4］,f(x)+
x3-4x+4≥m恒成立,求m的取值范围.
解:(1)令y=|2x+1|-|x-4|,则y=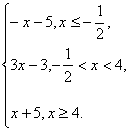
作出函数y=|2x+1|-|x-4|的图象,它与直线y=2的交点为(-7,2)和(
,2).
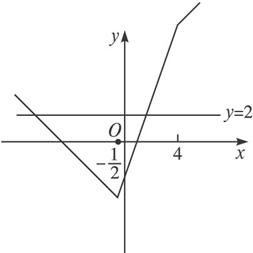
所以|2x+1|-|x-4|＞2的解集为(-∞,-7)∪(
,+∞).
(2)x∈［-1,4］,f(x)=3x-3.
原不等式恒成立,即
x3-x+1≥m恒成立.
令g(x)=
x3-x+1,
g′(x)=x2-1,因此g(x)在［-1,1］上是减函数,在(1,4］上是增函数,
又g(-1)=
,g(1)=
,g(4)=
.
所以,g(x)的最小值为
,即m≤1.
练习册系列答案
相关题目
设函数f(x)=2
，对于给定的正数K，定义函数fK(x)=
若对于函数f(x)=2
定义域内的任意 x，恒有fK（x）=f（x），则（ ）
| -x2+x+2 |
|
| -x2+x+2 |
A、K的最大值为2
| ||
B、K的最小值为2
| ||
| C、K的最大值为1 | ||
| D、K的最小值为1 |