Question

（本小题满分13分）

为加强大学生实践、创新能力和团队精神的培养，促进高等教育教学改革，教育部门主办了全国大学生智能汽车竞赛. 该竞赛分为预赛和决赛两个阶段，参加决赛的队伍按照抽签方式决定出场顺序.通过预赛，选拔出甲、乙等五支队伍参加决赛.

（Ⅰ）求决赛中甲、乙两支队伍恰好排在前两位的概率；

（Ⅱ）若决赛中甲队和乙队之间间隔的队伍数记为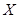，求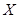的分布列和数学期望.

 

 

Answer 1

【答案】

(16)（本小题满分13分）

解：（Ⅰ）设“甲、乙两支队伍恰好排在前两位”为事件，则

.                      ………………………………………4分

所以 甲、乙两支队伍恰好排在前两位的概率为.

………………………………………5分

（Ⅱ）随机变量的可能取值为.  ………………………………………6分

，

，[来源:学.科.网]

，

.                ………………………………………10分

随机变量的分布列为：

因为 ，

所以 随机变量的数学期望为.         ………………………………………13分

 

 

【解析】略