题目内容
已知椭圆C: 的左,右焦点分别为
的左,右焦点分别为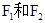 ,过
,过 的直线L与椭圆C相交 A,B于两点,且直线L的倾斜角为
的直线L与椭圆C相交 A,B于两点,且直线L的倾斜角为 ,点
,点 到直线L的距离为
到直线L的距离为 ,
,
(1) 求椭圆C的焦距.(2)如果 求椭圆C的方程.(12分)
求椭圆C的方程.(12分)
(1)焦距2c=4(2)椭圆C的方程为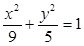 。
。
解析试题分析:(1)由点到直线的距离公式可求出c=2.从而得到焦距2c=4.
(2) 因为直线l过点F2(2,0),可设直线L的方程为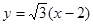 ,它与椭圆的方程联立消去x得到关于y的一元二次方程,再利用韦达定理,得到y1+y2,y1y2,然后再利用
,它与椭圆的方程联立消去x得到关于y的一元二次方程,再利用韦达定理,得到y1+y2,y1y2,然后再利用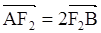 ,
,
得到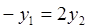 ,这三个式子结合可求出a,b.从而得到椭圆的方程.
,这三个式子结合可求出a,b.从而得到椭圆的方程.
(1)∵点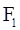 到直线L的距离为
到直线L的距离为 ,∴易得
,∴易得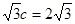 ,∴c=2
,∴c=2
∴焦距2c=4(5分).
(2)∵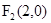 ,又过
,又过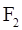 的直线L的倾斜角为
的直线L的倾斜角为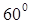 ,∴直线L的方程为
,∴直线L的方程为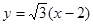 ,
,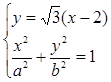 得
得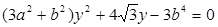 设
设 ,
, ,解得
,解得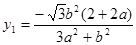 ,
,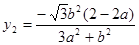
∵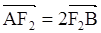 ,∴
,∴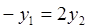 ,∴a="3," ∴
,∴a="3," ∴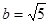 .
.
椭圆C的方程为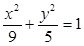 (12分)
(12分)
考点:点到直线的距离,直线与椭圆的方程的位置关系.
点评:(1)本题涉及到点到直线的距离公式: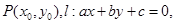 则点P到直线l的距离
则点P到直线l的距离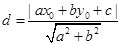 .
.
(2)直线与圆锥曲线的位置关系问题一般要通过韦达定理及判别式来解决.

练习册系列答案
相关题目
 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为 ,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为 。
。
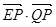 的取值范围.
的取值范围.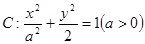 的左、右顶点分别为
的左、右顶点分别为 、
、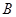 ,点
,点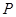 在椭圆上且异于
在椭圆上且异于 为坐标原点.
为坐标原点.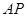 与
与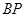 的斜率之积为
的斜率之积为 ,求椭圆的离心率;
,求椭圆的离心率; ,过点
,过点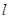 交
交 轴于点
轴于点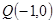 ,交
,交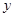 轴于点
轴于点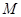 ,若
,若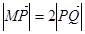 ,求直线
,求直线 为双曲线
为双曲线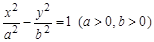 的左、右焦点.
的左、右焦点.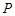 为双曲线与圆
为双曲线与圆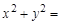
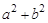 的一个交点,且满足
的一个交点,且满足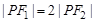 ,求此双曲线的离心率;
,求此双曲线的离心率;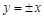 ,
, 到渐近线的距离是
到渐近线的距离是 ,过
,过 轴相切,求线段AB的长.
轴相切,求线段AB的长.  与抛物线
与抛物线 交于不同两点A、B,F为抛物线的焦点。
交于不同两点A、B,F为抛物线的焦点。 的重心G的轨迹方程;
的重心G的轨迹方程; 的外接圆的方程。
的外接圆的方程。 的坐标分别为
的坐标分别为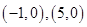 ,直线
,直线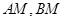 相交于点
相交于点 ,且它们的斜率之积是
,且它们的斜率之积是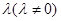 ,试讨论点
,试讨论点 ,且点A
,且点A 和点B
和点B 都在椭圆
都在椭圆 内部,
内部, 的所有可能结果;
的所有可能结果;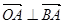 成立的
成立的 O
O 中,直线
中,直线 与抛物线
与抛物线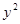 =2
=2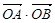 =3”是真命题;
=3”是真命题;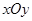 中,椭圆
中,椭圆 为
为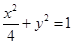
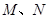 ,且线段
,且线段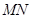 恰以点
恰以点 为中点,求直线
为中点,求直线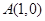 的直线
的直线 (非
(非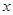 轴)与椭圆
轴)与椭圆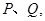 试问在
试问在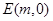 ,使
,使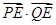 恒为定值
恒为定值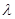 ?若存在,求出点
?若存在,求出点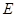 的坐标及实数
的坐标及实数