题目内容
定义在(-1,1)上的函数f(x)满足:f(x)-f(y)=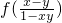 ;当x∈(-1,0)时,有f(x)>0;若P=
;当x∈(-1,0)时,有f(x)>0;若P=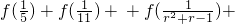
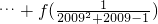 ,Q=f(
,Q=f( ),R=f(0);则P,Q,R的大小关系为
),R=f(0);则P,Q,R的大小关系为
- A.R>Q>P
- B.P>R>Q
- C.R>P>Q
- D.不能确定
C
分析:函数f(x)满足:f(x)-f(y)=f( );当x∈(-1,0)时,有f(x)>0;证明函数是奇函数,以及它的单调性,根据f(
);当x∈(-1,0)时,有f(x)>0;证明函数是奇函数,以及它的单调性,根据f(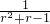 )=f(
)=f(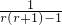 )=f(
)=f(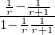 )=f(
)=f(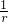 )-f(
)-f( )对p进行化简,再根据单调性比较P,Q,R的大小.
)对p进行化简,再根据单调性比较P,Q,R的大小.
解答:∵函数f(x)满足:f(x)-f(y)=f( );当x∈(-1,0)时,有f(x)>0;
);当x∈(-1,0)时,有f(x)>0;
∴f(x)在(-1,1)为奇函数,单调减函数,且在(-1,0)时,f(x)>0,在(0,1)时f(x)<0;∴R=f(0)=0,Q=f( )<0<R,
)<0<R,
∵f(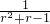 )=f(
)=f(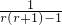 )=f(
)=f(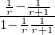 )=f(
)=f(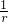 )-f(
)-f( ),
),
∴P=f( )+f(
)+f( )+…+f(
)+…+f( )+…+f(
)+…+f(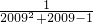 ),Q=f(
),Q=f( ),
),
=[f( )-f(
)-f( )]+[f(
)]+[f( )-f(
)-f( )]+…+[f(
)]+…+[f( )-f(
)-f( )]=f(
)]=f( )-f(
)-f( )
)
=Q-f( )>Q,
)>Q,
P=f( )-f(
)-f( )<0<R,
)<0<R,
故选C.
点评:对于抽象函数的解决方法,通常采取赋值法,把抽象的数学问题转化为熟悉的数学问题加以解决,命题的立意新,特别是对P=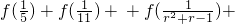
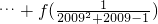 转化是难点,属中档题.
转化是难点,属中档题.
分析:函数f(x)满足:f(x)-f(y)=f(
 );当x∈(-1,0)时,有f(x)>0;证明函数是奇函数,以及它的单调性,根据f(
);当x∈(-1,0)时,有f(x)>0;证明函数是奇函数,以及它的单调性,根据f(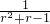 )=f(
)=f(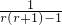 )=f(
)=f(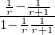 )=f(
)=f(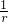 )-f(
)-f( )对p进行化简,再根据单调性比较P,Q,R的大小.
)对p进行化简,再根据单调性比较P,Q,R的大小.解答:∵函数f(x)满足:f(x)-f(y)=f(
 );当x∈(-1,0)时,有f(x)>0;
);当x∈(-1,0)时,有f(x)>0;∴f(x)在(-1,1)为奇函数,单调减函数,且在(-1,0)时,f(x)>0,在(0,1)时f(x)<0;∴R=f(0)=0,Q=f(
 )<0<R,
)<0<R,∵f(
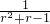 )=f(
)=f(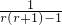 )=f(
)=f(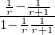 )=f(
)=f(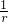 )-f(
)-f( ),
),∴P=f(
 )+f(
)+f( )+…+f(
)+…+f( )+…+f(
)+…+f(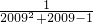 ),Q=f(
),Q=f( ),
),=[f(
 )-f(
)-f( )]+[f(
)]+[f( )-f(
)-f( )]+…+[f(
)]+…+[f( )-f(
)-f( )]=f(
)]=f( )-f(
)-f( )
)=Q-f(
 )>Q,
)>Q,P=f(
 )-f(
)-f( )<0<R,
)<0<R,故选C.
点评:对于抽象函数的解决方法,通常采取赋值法,把抽象的数学问题转化为熟悉的数学问题加以解决,命题的立意新,特别是对P=
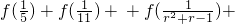
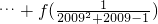 转化是难点,属中档题.
转化是难点,属中档题. 
练习册系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.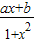 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.