题目内容
已知 ,则tanα的值为
,则tanα的值为
- A.-
 或-
或-
- B.
 或
或
- C.-

- D.-

C
分析:通过sinα+cosα= ,求出sinαcosα的值,再给式子添上一个分母1,把1变成角的正弦与余弦的平方和,分子和分母同除以余弦的平方,得到关于正切的方程,根据判断的角的范围求出结果.
,求出sinαcosα的值,再给式子添上一个分母1,把1变成角的正弦与余弦的平方和,分子和分母同除以余弦的平方,得到关于正切的方程,根据判断的角的范围求出结果.
解答:∵sinα+cosα= ,
,
所以2sinαcosα=- ,
,
∴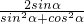 =-
=- ,
,
∴
∴12tan2α+25tanα+12=0
根据得到的角的范围得到tan
故选C
点评:本题考查三角函数的化简求值,正弦、余弦函数化为正切,即同角三角函数的基本关系式的应用,本题解题的关键是弦化切,本题是一个基础题.
分析:通过sinα+cosα=
 ,求出sinαcosα的值,再给式子添上一个分母1,把1变成角的正弦与余弦的平方和,分子和分母同除以余弦的平方,得到关于正切的方程,根据判断的角的范围求出结果.
,求出sinαcosα的值,再给式子添上一个分母1,把1变成角的正弦与余弦的平方和,分子和分母同除以余弦的平方,得到关于正切的方程,根据判断的角的范围求出结果.解答:∵sinα+cosα=
 ,
,所以2sinαcosα=-
 ,
,
∴
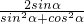 =-
=- ,
,∴

∴12tan2α+25tanα+12=0
根据得到的角的范围得到tan

故选C
点评:本题考查三角函数的化简求值,正弦、余弦函数化为正切,即同角三角函数的基本关系式的应用,本题解题的关键是弦化切,本题是一个基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知![]() ,则tanα的值为( )
,则tanα的值为( )
|
| A. | ﹣ | B. |
| C. | ﹣ | D. | ﹣ |
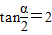 ,则tanα的值为 .
,则tanα的值为 .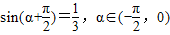 ,则tanα的值为( )
,则tanα的值为( )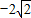
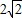
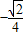
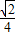
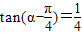 ,则tanα的值为( )
,则tanα的值为( )
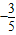


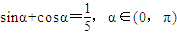 ,则tanα的值为( )
,则tanα的值为( ) 或-
或-
 或
或

