题目内容
P是椭圆 上的动点, 作PD⊥y轴, D为垂足, 则PD中点的轨迹方程为 ( )
上的动点, 作PD⊥y轴, D为垂足, 则PD中点的轨迹方程为 ( )
A 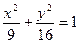 B
B  C
C 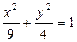 D
D 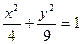
D
解析

练习册系列答案
相关题目
设集合A={1,2,3,4},m,n∈A,则方程 表示焦点在x轴上的椭圆有
表示焦点在x轴上的椭圆有
| A.6个 | B.8个 | C.12个 | D.16个 |
曲线 与曲线
与曲线 的
的
| A.长轴长相等 | B.短轴长相等 | C.离心率相等 | D.焦距相等 |
椭圆 的离心率为
的离心率为
A. | B. | C. | D. |
若一个椭圆的长轴、短轴长度和焦距成等差数列,则该椭圆的离心率是
A. | B. | C. | D. |
在一椭圆中以焦点 为直径两端点的圆,恰好过短轴的两顶点,则此椭圆的离心率
为直径两端点的圆,恰好过短轴的两顶点,则此椭圆的离心率 等于 ( )
等于 ( )
A. | B. | C. | D. |
若 为双曲线
为双曲线 上一点,
上一点, 、
、 分别为双曲线的左右焦点,且
分别为双曲线的左右焦点,且 ,则
,则 ( )
( )
| A.2或6 | B.6 | C.2 | D.7 |
已知双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )
A. | B. | C. | D. |
 是方程
是方程  表示椭圆或双曲线的( )
表示椭圆或双曲线的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.不充分不必要条件 |