Question

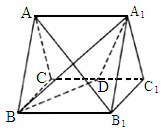
(2007福建，18)如下图，正三棱柱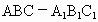的所有棱长都为2，D为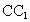中点．

(1)求证：⊥平面；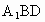

(2)求二面角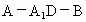的大小；

(3)求点C到平面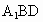的距离．

Answer 1

答案：略
解析：

解析：解法一：(1)取BC中点O，连接AO． ∵△ABC为正三角形，∴AO⊥BC． ∵正三棱柱中，平面ABC⊥平面， ∴AO⊥平面． 连结，在正方形中，O、D分别为BC、的中点， ∴，∴． 在正方形中，， ． (2)设与交于点G，在平面中，作于F，连结AF，由(1)得 ， ∴， ∴∠AFG为二面角的平面角． 在中，由等面积法可求得 ，又∵， ∴， 所以二面角的大小为． (3)中，，，∴． ． 在正三棱柱中，到平面的距离为． 设点C到平面的距离为d． 由得， ∴． ∴点C到平面的距离为． 解法二：(1)取BC中点O，连结AO． ∵△ABC为正三角形，∴AO⊥BC． ∵在正三棱柱中，平面ABC⊥平面， ∴AO⊥平面． 取中点，以O为原点，，，的方向为x、y、z轴的正方向建立空间直角坐标系，则B(1，0，0)，D(－1，1，0)，，A(0，0，)，(1，2，0)， ∴，，． ∵，， ∴， ∴⊥平面． (2)设平面的法向量为n=(x，y，z)． ，=(0，2，0)． ∵，， ∴∴ ∴ 令z=1得为平面的一个法向量． 由(1)知平面， ∴为平面的法向量． ． ∴二面角的大小为． (3)由(2)，法向量． ∵=(－2，0，0)，， ∴点C到平面的距离．