题目内容
(本小题满分10分)
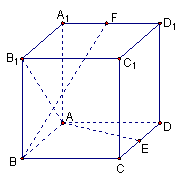 在正方体
在正方体![]() 中,E,F分别是CD,A1D1中点
中,E,F分别是CD,A1D1中点
(1)求证:AB1⊥BF;
(2)求证:AE⊥BF;
(3)棱CC1上是否存在点P,使BF⊥平面AEP,若存在,
确定点P的位置;若不存在,说明理由
解:(1)证明:连结A1B,CD1 ∵AB1⊥A1B, AB1⊥BC,A1B∩BC=B ∴AB1⊥平面A1BCD1 , 又BF![]() 平面A1BCD1 ,所以AB1⊥BF
平面A1BCD1 ,所以AB1⊥BF
(2) 证明:取AD中点M,连结FM,BM ∵ABCD为正方形,E,M分别为所在棱的中点,
∴AE⊥BM,又∵FM⊥AE,BM∩FM=M, ∴AE⊥平面BFM, 又BF![]() 平面BFM,∴AE⊥BF
平面BFM,∴AE⊥BF
(3) 存在,P是CC1的中点,则易证PE∥AB1,故A,B1,E,P四点共面
证明:由(1)(2)知AB1⊥BF,AE⊥BF,AB1∩AE=A,∴BF⊥平面AEB1, 即BF⊥平面AEP

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,