题目内容
若函数y=
的值域为（－∞，
）∪[1，+∞），求实数a、b的值。
答案：
解析：
解析：
由y= ，
得yx2+(y－a)x－(y+b)=0.∵x∈R，∴△=（y－a）2+4y(y+b)≥0， 即5y2+(4b－2a)y+a2≥0. ① 又由函数的值域为（－∞， ∴
|
]∪[1，+∞），∴关于y的不等式①的解为y≤
或y≥1。
故所求的值为
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
，给出以下四个命题，其中真命题是（ ）
, 则函数y的值域为
； B．在区间
上是增函数;
是函数图象的一条对称轴; 
的图象按向量
=(
,0)平移后而得到.
的值域为(－∞,
］∪［1,+∞)，求实数a、b的值.
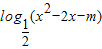的值域为R；
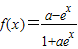在定义域上是奇函数”的充分不必要条件．
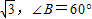，AB=1的三角形△ABC有两个．