题目内容
已知在区间(a,b)上,f(x)>0,f′(x)>0,对x轴上的任意两点(x1,0),(x2,0),(a<x1<x2<b)都有f( )>
)> .若S1=
.若S1= f(x)dx,S2=
f(x)dx,S2= (b-a),S3=f(a)(b-a),则S1、S2、S3的大小关系为 .
(b-a),S3=f(a)(b-a),则S1、S2、S3的大小关系为 .
【答案】分析:根据题中条件:”对x轴上的任意两点(x1,0),(x2,0),(a<x1<x2<b)都有f( )>
)> .”知函数图象是上凸的,结合图形可得S1、S2、S3的大小关系.
.”知函数图象是上凸的,结合图形可得S1、S2、S3的大小关系.
解答: 解析:根据定积分的几何意义知:
解析:根据定积分的几何意义知:
S1为f(x)的图象与直线x=a,x=b及x轴围成的曲边梯形的面积,
而s2为梯形的面积,s3为矩形的面积,
所以结合题意并画出图形可得S1>S2>S3.
故答案为:S1>S2>S3.
点评:本题考查了定积分的简单应用,以及数形结合思想的综合应用,属于基础题.解决时要注意数形结合思想应用.
 )>
)> .”知函数图象是上凸的,结合图形可得S1、S2、S3的大小关系.
.”知函数图象是上凸的,结合图形可得S1、S2、S3的大小关系.解答:
 解析:根据定积分的几何意义知:
解析:根据定积分的几何意义知:S1为f(x)的图象与直线x=a,x=b及x轴围成的曲边梯形的面积,
而s2为梯形的面积,s3为矩形的面积,
所以结合题意并画出图形可得S1>S2>S3.
故答案为:S1>S2>S3.
点评:本题考查了定积分的简单应用,以及数形结合思想的综合应用,属于基础题.解决时要注意数形结合思想应用.

练习册系列答案
相关题目
 )>
)> .若S1=
.若S1= f(x)dx,S2=
f(x)dx,S2= (b-a),S3=f(a)(b-a),则S1、S2、S3的大小关系为 .
(b-a),S3=f(a)(b-a),则S1、S2、S3的大小关系为 . )>
)> .若S1=
.若S1= f(x)dx,S2=
f(x)dx,S2= (b-a),S3=f(a)(b-a),则S1、S2、S3的大小关系为 .
(b-a),S3=f(a)(b-a),则S1、S2、S3的大小关系为 . )>
)>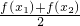 .若S1=
.若S1= f(x)dx,S2=
f(x)dx,S2= (b-a),S3=f(a)(b-a),则S1、S2、S3的大小关系为________.
(b-a),S3=f(a)(b-a),则S1、S2、S3的大小关系为________.