题目内容
已知椭圆| (x-c)2+y2 |
| (x+c)2+y2 |
分析:利用点到直线的距离公式求出圆心(0,0)到直线的距离,代入弦长公式求出弦长.
解答:解:∵
+
=10
∴a=5,b2+c2=25,
圆心(0,0)到直线bx+cy+3=0的距离等于d=
=
,
由弦长公式得弦长为2
=2
=
,
故答案为:
.
| (x-c)2+y2 |
| (x+c)2+y2 |
∴a=5,b2+c2=25,
圆心(0,0)到直线bx+cy+3=0的距离等于d=
| |0+0+3| | ||
|
| 3 |
| 5 |
由弦长公式得弦长为2
| r2-d2 |
1-
|
| 8 |
| 5 |
故答案为:
| 8 |
| 5 |
点评:本题考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,求出圆心(0,0)到直线的距离是解题的关键,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知直线x-2y+2=0经过椭圆
已知直线x-2y+2=0经过椭圆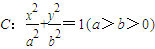 的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AS,BS与直线
的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AS,BS与直线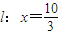 分别交于M,N两点.
分别交于M,N两点. ?若存在,确定点T的个数,若不存在,说明理由.
?若存在,确定点T的个数,若不存在,说明理由.
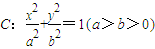 的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AS,BS与直线
的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AS,BS与直线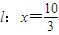 分别交于M,N两点.
分别交于M,N两点. ?若存在,确定点T的个数,若不存在,说明理由.
?若存在,确定点T的个数,若不存在,说明理由.