题目内容
已知双曲线x2-y2=2的左、右焦点分别为F1,F2,过点F2的动直线与双曲线相交于A,B两点.(I)若动点M满足
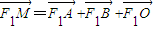 (其中O为坐标原点),求点M的轨迹方程;
(其中O为坐标原点),求点M的轨迹方程;(II)在x轴上是否存在定点C,使
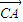 •
•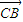 为常数?若存在,求出点C的坐标;若不存在,请说明理由.
为常数?若存在,求出点C的坐标;若不存在,请说明理由.
【答案】分析:(1)先根据条件求出左、右焦点的坐标,并设A(x1,y1),B(x2,y2),M(x,y),然后表示出向量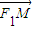 ,
,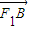 ,
,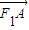 ,
,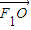 ,根据
,根据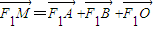 可得到x1,x2,x以及y1,y2,y的关系,即可表示出AB的中点坐标,然后分AB不与x轴垂直和AB与x轴垂直两种情况进行讨论.
可得到x1,x2,x以及y1,y2,y的关系,即可表示出AB的中点坐标,然后分AB不与x轴垂直和AB与x轴垂直两种情况进行讨论.
(2)假设在x轴上存在定点C(m,0),使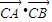 为常数,当AB不与x轴垂直时,设出直线AB的方程,然后与双曲线方程联立消去y得到关于x的一元二次方程,进而可得到两根之和与两根之积,表示出向量
为常数,当AB不与x轴垂直时,设出直线AB的方程,然后与双曲线方程联立消去y得到关于x的一元二次方程,进而可得到两根之和与两根之积,表示出向量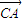 •
•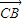 并将所求的两根之和与两根之积代入整理即可求出C的坐标;当AB与x轴垂直时可直接得到A,B的坐标,再由
并将所求的两根之和与两根之积代入整理即可求出C的坐标;当AB与x轴垂直时可直接得到A,B的坐标,再由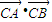 =-1,可确定答案.
=-1,可确定答案.
解答:解:由条件知F1(-2,0),F2(2,0),设A(x1,y1),B(x2,y2)
(I)设M(x,y),则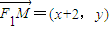 ,
,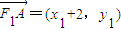 ,
,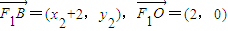 ,
,
由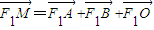 ,得
,得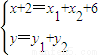 ,即
,即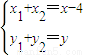 ,
,
于是AB的中点坐标为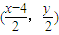 ,
,
当AB不与x轴垂直时,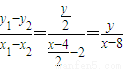 ,即
,即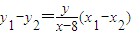 ,
,
又因为A,B两点在双曲线上,所以x12-y12=2,x22-y22=2,
两式相减得(x1-x2)(x1+x2)=(y1-y2)(y1+y2),即(x1-x2)(x-4)=(y1-y2)y,
将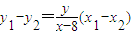 代入上式,化简得(x-6)2-y2=4,
代入上式,化简得(x-6)2-y2=4,
当AB与x轴垂直时,x1=x2=2,求得M(8,0),也满足上述方程,
所以点M的轨迹方程是(x-6)2-y2=4.
(II)假设在x轴上存在定点C(m,0),使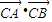 为常数,
为常数,
当AB不与x轴垂直时,设直线AB的方程是y=k(x-2)(k≠±1),
代入x2-y2=2有(1-k2)x2+4k2x-(4k2+2)=0
则x1,x2是上述方程的两个实根,所以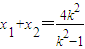 ,
,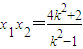 ,
,
于是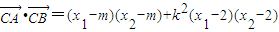
=(k2+1)x1x2-(2k2+m)(x1+x2)+4k2+m2
=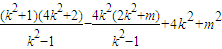
=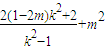
=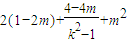 .
.
因为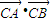 是与k无关的常数,所以4-4m=0,即m=1,此时
是与k无关的常数,所以4-4m=0,即m=1,此时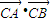 =-1,
=-1,
当AB与x轴垂直时,点A,B的坐标可分别设为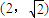 ,
,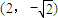 ,
,
此时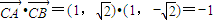 ,
,
故在x轴上存在定点C(1,0),使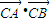 为常数.
为常数.
点评:本题主要考查直线与双曲线的综合问题.直线与圆锥曲线的综合题是高考的热点问题,每年必考,要强化复习.
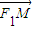 ,
,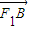 ,
,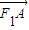 ,
,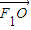 ,根据
,根据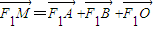 可得到x1,x2,x以及y1,y2,y的关系,即可表示出AB的中点坐标,然后分AB不与x轴垂直和AB与x轴垂直两种情况进行讨论.
可得到x1,x2,x以及y1,y2,y的关系,即可表示出AB的中点坐标,然后分AB不与x轴垂直和AB与x轴垂直两种情况进行讨论.(2)假设在x轴上存在定点C(m,0),使
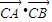 为常数,当AB不与x轴垂直时,设出直线AB的方程,然后与双曲线方程联立消去y得到关于x的一元二次方程,进而可得到两根之和与两根之积,表示出向量
为常数,当AB不与x轴垂直时,设出直线AB的方程,然后与双曲线方程联立消去y得到关于x的一元二次方程,进而可得到两根之和与两根之积,表示出向量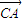 •
•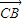 并将所求的两根之和与两根之积代入整理即可求出C的坐标;当AB与x轴垂直时可直接得到A,B的坐标,再由
并将所求的两根之和与两根之积代入整理即可求出C的坐标;当AB与x轴垂直时可直接得到A,B的坐标,再由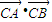 =-1,可确定答案.
=-1,可确定答案.解答:解:由条件知F1(-2,0),F2(2,0),设A(x1,y1),B(x2,y2)
(I)设M(x,y),则
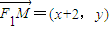 ,
,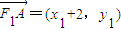 ,
,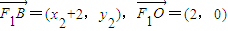 ,
,由
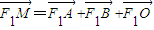 ,得
,得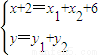 ,即
,即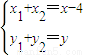 ,
,于是AB的中点坐标为
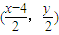 ,
,当AB不与x轴垂直时,
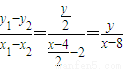 ,即
,即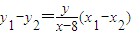 ,
,又因为A,B两点在双曲线上,所以x12-y12=2,x22-y22=2,
两式相减得(x1-x2)(x1+x2)=(y1-y2)(y1+y2),即(x1-x2)(x-4)=(y1-y2)y,
将
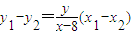 代入上式,化简得(x-6)2-y2=4,
代入上式,化简得(x-6)2-y2=4,当AB与x轴垂直时,x1=x2=2,求得M(8,0),也满足上述方程,
所以点M的轨迹方程是(x-6)2-y2=4.
(II)假设在x轴上存在定点C(m,0),使
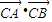 为常数,
为常数,当AB不与x轴垂直时,设直线AB的方程是y=k(x-2)(k≠±1),
代入x2-y2=2有(1-k2)x2+4k2x-(4k2+2)=0
则x1,x2是上述方程的两个实根,所以
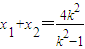 ,
,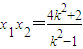 ,
,于是
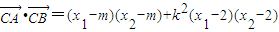
=(k2+1)x1x2-(2k2+m)(x1+x2)+4k2+m2
=
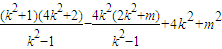
=
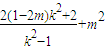
=
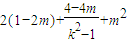 .
.因为
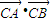 是与k无关的常数,所以4-4m=0,即m=1,此时
是与k无关的常数,所以4-4m=0,即m=1,此时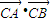 =-1,
=-1,当AB与x轴垂直时,点A,B的坐标可分别设为
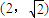 ,
,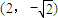 ,
,此时
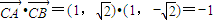 ,
,故在x轴上存在定点C(1,0),使
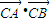 为常数.
为常数.点评:本题主要考查直线与双曲线的综合问题.直线与圆锥曲线的综合题是高考的热点问题,每年必考,要强化复习.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知双曲线x2-y2=a2(a>0)的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P,∠PAB=α,∠PBA=β,∠APB=γ,则( )
| A、tanα+tanβ+tanγ=0 | B、tanα+tanβ-tanγ=0 | C、tanα+tanβ+2tanγ=0 | D、tanα+tanβ-2tanγ=0 |