题目内容
已知mx2+mx+m＜1的解集为R，则m的取值范围是（ ）
分析：对m分类讨论．①当m=0时，直接验证即可；②当m≠0时，要使mx2+mx+m-1＜0的解集为R，必须满足
，解得即可．
|
解答：解：①当m=0时，mx2+mx+m＜1化为0＜1，其解集为R，满足条件；
②当m≠0时，要使mx2+mx+m-1＜0的解集为R，必须满足
，解得m＜0．
综上可知：m的取值范围是（-∞，0]．
故选C．
②当m≠0时，要使mx2+mx+m-1＜0的解集为R，必须满足
|
综上可知：m的取值范围是（-∞，0]．
故选C．
点评：熟练掌握分类讨论、一元二次不等式的解集与△及二次项的系数的关系是解题的关键．
练习册系列答案
相关题目
Q
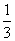x3-mx2+
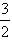mx(m＞0)，
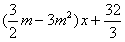恒成立，求m的取值范围。