题目内容
(本小题满分12分)已知 的顶点
的顶点 ,
, 边上的中线
边上的中线 所在的直线方程为
所在的直线方程为 ,
, 边上的高
边上的高 所在直线的方程为
所在直线的方程为 .
.
(1)求 的顶点
的顶点 、
、 的坐标;
的坐标;
(2)若圆 经过
经过 、
、 且与直线
且与直线 相切于点
相切于点 (-3,0),求圆
(-3,0),求圆
 的方程.
的方程.
 的顶点
的顶点 ,
, 边上的中线
边上的中线 所在的直线方程为
所在的直线方程为 ,
, 边上的高
边上的高 所在直线的方程为
所在直线的方程为 .
.(1)求
 的顶点
的顶点 、
、 的坐标;
的坐标;(2)若圆
 经过
经过 、
、 且与直线
且与直线 相切于点
相切于点 (-3,0),求圆
(-3,0),求圆
 的方程.
的方程.解:(1) 边上的高
边上的高 所在直线的方程为
所在直线的方程为 ,所以,
,所以,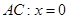 ,
,
又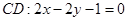 ,所以,
,所以,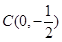 ,设
,设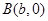 ,则
,则 的中点
的中点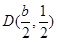 ,代入方程
,代入方程 ,解得
,解得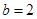 ,所以
,所以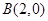 . (4分)
. (4分)
(2)由 ,
,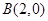 可得,圆
可得,圆 的弦
的弦 的中垂线方程为
的中垂线方程为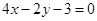 ,①
,①
由与x-y+3=0相切,切点为(-3,0)可得,圆心所在直线为y+x+3=0,②
① ②联立可得,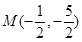 , (8分)
, (8分)
半径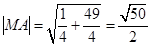 ,所以所求圆方程为
,所以所求圆方程为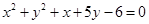 。 (12分)
。 (12分)
 边上的高
边上的高 所在直线的方程为
所在直线的方程为 ,所以,
,所以,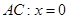 ,
,又
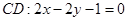 ,所以,
,所以,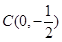 ,设
,设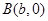 ,则
,则 的中点
的中点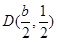 ,代入方程
,代入方程 ,解得
,解得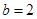 ,所以
,所以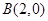 . (4分)
. (4分)(2)由
 ,
,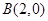 可得,圆
可得,圆 的弦
的弦 的中垂线方程为
的中垂线方程为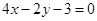 ,①
,①由与x-y+3=0相切,切点为(-3,0)可得,圆心所在直线为y+x+3=0,②
① ②联立可得,
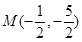 , (8分)
, (8分)半径
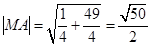 ,所以所求圆方程为
,所以所求圆方程为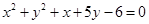 。 (12分)
。 (12分)略

练习册系列答案
相关题目
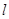 过点
过点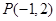 ,且点
,且点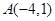 ,
,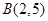 到直线
到直线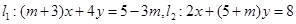 相交,则
相交,则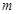 的取值是
的取值是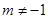
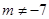
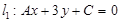 与
与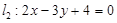 ,若
,若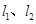 的交点在
的交点在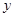 轴上,则
轴上,则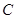 的值为
的值为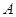 的取值有关
的取值有关 当
当 时,则
时,则 等于( )
等于( )

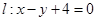 与圆
与圆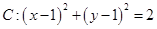 ,则
,则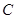 上各点到
上各点到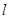 的距离的最小值为___ _
的距离的最小值为___ _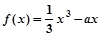 的切线,则实数a的取值范围是____________
的切线,则实数a的取值范围是____________