题目内容
已知H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点T(-1,0)作直线l与轨迹C交于A、B两点,若在x轴上存在一点E(x0,0),使得△ABE是等边三角形,求x0的值.
分析:(1)设出M的坐标,利用题意向量的关系,求得x和y的关系,进而求得M的轨迹C.
(2)设直线l的方程,代入抛物线方程,设出A,B的坐标,利用韦达定理表示出x1+x2和x1x2,则线段AB中点坐标以及AB的中垂线的方程可得,把y=0代入方程,最后利用△ABE为正三角形,利用正三角的性质推断E到直线AB的距离的关系式求得k,则x0可求.
(2)设直线l的方程,代入抛物线方程,设出A,B的坐标,利用韦达定理表示出x1+x2和x1x2,则线段AB中点坐标以及AB的中垂线的方程可得,把y=0代入方程,最后利用△ABE为正三角形,利用正三角的性质推断E到直线AB的距离的关系式求得k,则x0可求.
解答:解(1)设点M的坐标为(x,y),
由
=-
.得P(0,-
),Q(
,0),
由
•
=0,得(3,-
)•(x,
)=0,
所以y2=4x由点Q在x轴的正半轴上,得x>0,
所以,动点M的轨迹C是以(0,0)为顶点,以(1,0)为焦点的抛物线,除去原点.
(2)设直线l:y=k(x+1),其中k≠0代入y2=4x,得k2x2+2(k2-2)x+k2=0①
设A(x1,y1),B(x2,y2),则x1,x2是方程①的两个实数根,由韦达定理得x1+x2=-
,x1x2=1
所以,线段AB的中点坐标为(
,
),线段AB的垂直平分线方程为y-
=-
(x-
),
令y=0,x0=
+1,所以,点E的坐标为(
+1,0).
因为△ABE为正三角形,所以,点E(
+1,0)到直线AB的距离等于
|AB|,而|AB|=
=
•
.
所以,
=
解得k=±
,所以x0=
.
由
| PM |
| 3 |
| 2 |
| MQ |
| y |
| 2 |
| x |
| 3 |
由
| HP |
| PM |
| y |
| 2 |
| 3y |
| 2 |
所以y2=4x由点Q在x轴的正半轴上,得x>0,
所以,动点M的轨迹C是以(0,0)为顶点,以(1,0)为焦点的抛物线,除去原点.
(2)设直线l:y=k(x+1),其中k≠0代入y2=4x,得k2x2+2(k2-2)x+k2=0①
设A(x1,y1),B(x2,y2),则x1,x2是方程①的两个实数根,由韦达定理得x1+x2=-
| 2(k2-2) |
| k2 |
所以,线段AB的中点坐标为(
| 2-k2 |
| k2 |
| 2 |
| k |
| 2 |
| k |
| 1 |
| k |
| 2-k2 |
| k2 |
令y=0,x0=
| 2 |
| k2 |
| 2 |
| k2 |
因为△ABE为正三角形,所以,点E(
| 2 |
| k2 |
| ||
| 2 |
| (x1-x2)2+(y1-y2)2 |
4
| ||
| k2 |
| 1+k2 |
所以,
2
| ||||
| k2 |
2
| ||
| |k| |
| ||
| 2 |
| 11 |
| 3 |
点评:本题主要考查了椭圆的应用,向量的基本性质.考查了学生分析问题和解决问题的能力.

练习册系列答案
相关题目
 .
.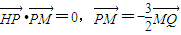 .
.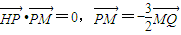 .
.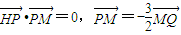 .
.