Question

在椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)中，F₁，F₂为其左、右焦点，以F₁F₂为直径的圆与椭圆交于A，B，C，D四个点，若F₁，F₂，A，B，C，D恰好为一个正六边形的六个顶点，则椭圆的离心率为（　　）

• A．

  2

  -1
• B．

  2

  2

• C．

  3

  -1
• D．

  3

  2

Answer 1

分析：如图，连接AF₂，结合正六边形的性质得∠F₁AF₂=90°．Rt△AF₁F₂中，|F₁F₂|=2c，|AF₁|=c，可得|AF₂|=

3

c，结合椭圆的定义得：|AF₁|+|AF₂|=（1+

3

）c=2a，再结合离心率公式即可算出该椭圆的离心率．

解答：解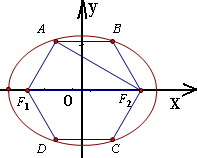：如图，连接AF₂，可得等腰△ABF₂中，∠B=120°
∴∠BAF₂=∠AF₂B=30°
因此∠F₁AF₂=120°-30°=90°
Rt△AF₁F₂中，|F₁F₂|=2c，|AF₁|=c
∴|AF₂|=

3

c，得|AF₁|+|AF₂|=（1+

3

）c=2a
因此，椭圆的离心率e=

c

a

=

2c

2a

=

2c

(1+ 3 )c

=

3

-1
故选：C

点评：本题给出椭圆的焦距恰好是其内接正六边形的长对角线，求椭圆的离心率，着重考查了椭圆的定义与基本概念、正六边形的性质等知识，属于基础题．