题目内容
18.已知关于x的方程x2-2x+k=0有两实数根x1,x2,设y=(x1+x2)(x12+x22-x1x2)2.(1)求y与k之间的函数关系式.
(2)试问y是否有最大值或最小值?若有,请求出,若没有,请说明理由.
分析 (1)根据根与系数之间的关系即可求y与k之间的函数关系式.
(2)结合一元二次函数的最值性质进行求解即可.
解答 解:(1)∵关于x的方程x2-2x+k=0有两实数根x1,x2,
∴判别式△=4-4k≥0,则k≤1,
且x1+x2=2,x1x2=k,
则y=(x1+x2)(x12+x22-x1x2)2=y=(x1+x2)[(x1+x2)2-3x1x2]2
=2(4-3k)2,k≤1,
即y=2(3k-4)2,k≤1.
(2)∵y=2(3k-4)2=18(k-$\frac{4}{3}$)2,k≤1.
对称轴为k=$\frac{4}{3}$,
∴当k≤1时,函数单调递减,
即当k=1时,函数取得最小值y=2,无最大值.
点评 本题主要考查函数最值的求解和判断,结合一元二次函数根与系数之间的关系以及一元二次函数的最值性质是解决本题的关键.

练习册系列答案
相关题目
9.若集合A={x|x=$\frac{k}{3}$,k∈Z},B={x|x=$\frac{k}{6}$,k∈Z},则( )
| A. | A$\underset{?}{≠}$B | B. | A$\underset{?}{≠}$B | C. | A=B | D. | A与B无公共元素 |
6.在一个文艺比赛中,12名专业人士和12名观众代表各组成一个评判小组,给参赛选手打分.下面是两个评判组对同一名选手的打分:
(1)解释如何衡量每一组成员的相似性.
(2)对每一组计算这种相似性的度量值.你能据此判断小组A与小组B哪一个更像是由专业人士组成的吗?
| 小组A | 42 | 45 | 48 | 46 | 52 | 47 | 49 | 55 | 42 | 51 | 47 | 45 |
| 小组B | 55 | 36 | 70 | 66 | 75 | 49 | 46 | 68 | 42 | 62 | 58 | 47 |
(2)对每一组计算这种相似性的度量值.你能据此判断小组A与小组B哪一个更像是由专业人士组成的吗?
13.设不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ y≤-kx+4k\end{array}\right.$在平面直角坐标系中所表示的区域的面积为S,则当k>1时,$\frac{kS}{k-1}$的最小值为( )
| A. | 16 | B. | 32 | C. | 48 | D. | 56 |
3.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2},x≥0}\\{{x}^{2}+2x,x<0}\end{array}\right.$,则不等式f(f(x))≤3的解集为( )
| A. | (-∞,1] | B. | (-∞,$\sqrt{2}$] | C. | (-∞,$\sqrt{3}$] | D. | (-∞,2] |
7.“a=2”是“{1,a}⊆{1,2,3}”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
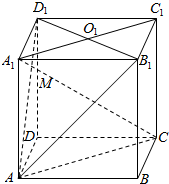 如图,O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点,求证:O1、M、A三点共线.
如图,O1是正方体ABCD-A1B1C1D1的面A1B1C1D1的中心,M是对角线A1C和截面B1D1A的交点,求证:O1、M、A三点共线.