题目内容
北京市各级各类中小学每年都要进行“学生体质健康测试”,测试总成绩满分为X分,规定测试成绩在X之间为体质优秀;在X之间为体质良好;在X之间为体质合格;在X之间为体质不合格.
现从某校高三年级的X名学生中随机抽取X名学生体质健康测试成绩,其茎叶图如下:
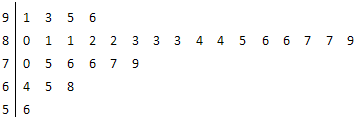
(Ⅰ)试估计该校高三年级体质为优秀的学生人数;
(Ⅱ)根据以上X名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取X名学生,再从这X名学生中选出X人.
(ⅰ)求在选出的X名学生中至少有X名体质为优秀的概率;
(ⅱ)记X为在选出的X名学生中体质为良好的人数,求X的分布列及数学期望.
现从某校高三年级的X名学生中随机抽取X名学生体质健康测试成绩,其茎叶图如下:
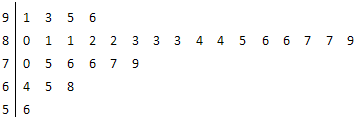
(Ⅰ)试估计该校高三年级体质为优秀的学生人数;
(Ⅱ)根据以上X名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取X名学生,再从这X名学生中选出X人.
(ⅰ)求在选出的X名学生中至少有X名体质为优秀的概率;
(ⅱ)记X为在选出的X名学生中体质为良好的人数,求X的分布列及数学期望.
分析:(Ⅰ)根据抽样的定义和条件即可估计该校高三年级体质为优秀的学生人数;
(Ⅱ)求出随机变量的分布列以及数学期望公式进行计算即可.
(Ⅱ)求出随机变量的分布列以及数学期望公式进行计算即可.
解答:解:(Ⅰ)根据抽样,估计该校高三学生中体质为优秀的学生人数有
×300=100人.
(Ⅱ)依题意,体质为良好和优秀的学生人数之比为 15:10=3:2.
所以,从体质为良好的学生中抽取的人数为
×5=3,从体质为优秀的学生中抽取的人数为
×5=2.
(ⅰ)设“在选出的3名学生中至少有名体质为优秀”为事件A,
则 P(A)=1-
=
. 故在选出的3名学生中至少有名体质为优秀的概率为
.
(ⅱ)解:随机变量X的所有取值为1,2,3.P(X=1)=
=
,P(X=2)=
=
,P(X=3)=
=
.
所以,随机变量X的分布列为:
EX=1×
+2×
+3×
=
.
| 10 |
| 30 |
(Ⅱ)依题意,体质为良好和优秀的学生人数之比为 15:10=3:2.
所以,从体质为良好的学生中抽取的人数为
| 3 |
| 5 |
| 2 |
| 5 |
(ⅰ)设“在选出的3名学生中至少有名体质为优秀”为事件A,
则 P(A)=1-
| ||
|
| 9 |
| 10 |
| 9 |
| 10 |
(ⅱ)解:随机变量X的所有取值为1,2,3.P(X=1)=
| ||||
|
| 3 |
| 10 |
| ||||
|
| 6 |
| 10 |
| ||
|
| 1 |
| 10 |
所以,随机变量X的分布列为:
| X | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 3 |
| 10 |
| 6 |
| 10 |
| 1 |
| 10 |
| 9 |
| 5 |
点评:本题主要考查茎叶图的应用以及随机变量的分布列和数学期望的计算,考查学生的计算能力.

练习册系列答案
相关题目











