题目内容

已知函数f(x)=x-ln(1+x)，数列{an}满足0＜a1＜1，an+1=f(an)；数列{bn}满足b1=，bn+1=(n+1)bn(n∈N*)

(Ⅰ)若x∈(0，1)求f(x)的值域；

(Ⅱ)求证：an+1＜；

(Ⅲ)若a1=，求证：当n≥2(n∈Z)时，ann!＜bn.

解：(Ⅰ)0＜x＜1时,f′(x)=1＞0,

所以f(x)在(0,1)上是增函数,f(0)＜f(x)＜f(1),即0＜f(x)＜1-ln2,

当x∈(0,1)时,f(x)的值域为(0,1-ln2). 

(Ⅱ)设函数g(x)=x-ln(1+x)(0＜x＜1),

则g′(x)=1＜0(0＜x＜1),

∴g(x)在(0,1)上递减.∵0＜a1＜1,由(Ⅰ)知0＜f(a1)＜1-ln2＜1,

即0＜a2＜1,同理a3,a4,…,an∈(0,1),

于是g(an)＜g(0)=0,即an-ln(1+an)＜0,故an+1＜. 

(Ⅲ)b1=,bn+1=(n+1)bn,n∈N*,所以bn＞0,且

bn==(n)[(n-1))[(n-2)]…(·2)=n!  

欲证ann！＜bn=n!,只需证an＜.

法一：数学归纳法

①当n=2时,由(Ⅱ)知a2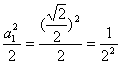＜,不等式成立.

②假设n=k(k≥2,k∈N*)时命题也成立,即ak＜.又由(Ⅱ)知0＜an＜1,

则n=k+1时,ak+1＜

由①②知当n≥2(n∈N*)时,不等式成立.

法二：当n≥2时,

an＜

因为n≥2所以n-1≥1,2n-1≥2.

∵0＜a1＜1,∴,∴an＜.


练习册系列答案
相关题目
已知函数f(x)=x-2m2+m+3(m∈Z)为偶函数，且f（3）＜f（5）．
（1）求m的值，并确定f（x）的解析式；
（2）若g（x）=loga[f（x）-ax]（a＞0且a≠1），是否存在实数a，使g（x）在区间[2，3]上的最大值为2，若存在，请求出a的值，若不存在，请说明理由．
（2011•上海模拟）已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．

已知函数f(x)的图像在[a，b]上连续不断，f1(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f2(x)＝max{f(t)|a≤t≤x}(x∈[a，b])，其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值，若存在最小正整数k，使得f2(x)－f1(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数f(x)为[a，b]上的“k阶收缩函数”．已知函数f(x)＝x2，x∈[－1，4]为[－1，4]上的“k阶收缩函数”，则k的值是_________．
已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f（x）、g（x），下列说法正确的是（ ）
A．f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数
B．f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数
C．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数
D．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网