题目内容
函数f（x）=x3+ax2+bx+a2在x=1处有极值10，则
- A.a=-11，b=4
- B.a=-4，b=11
- C.a=11，b=-4
- D.a=4，b=-11
D
分析：根据函数f（x）=x3+ax2+bx+a2在x=1处有极值10，可知f′（1）=0和f（1）=10，对函数f（x）求导，解方程组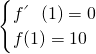
，注意验证，可求得答案．
解答：由f（x）=x3+ax2+bx+a2，
得f′（x）=3x2+2ax+b，
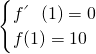，即
，
解得
或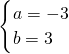
（经检验应舍去），
故选D．
点评：考查利用导数研究函数的极值问题，注意f′（x0）=0是x=x0是极值点的必要不充分条件，因此对于解得的结果要检验，这是易错点，属基础题．
分析：根据函数f（x）=x3+ax2+bx+a2在x=1处有极值10，可知f′（1）=0和f（1）=10，对函数f（x）求导，解方程组
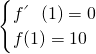，注意验证，可求得答案．解答：由f（x）=x3+ax2+bx+a2，
得f′（x）=3x2+2ax+b，
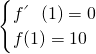，即，解得
或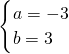（经检验应舍去），故选D．
点评：考查利用导数研究函数的极值问题，注意f′（x0）=0是x=x0是极值点的必要不充分条件，因此对于解得的结果要检验，这是易错点，属基础题．
练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目