题目内容
已知二次函数y=f(x)的图象经过坐标原点,其导函数为f'(x)=6x-2,数列{an}的前n项和为Sn,点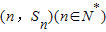 均在函数y=f(x)的图象上.
均在函数y=f(x)的图象上.(1)求y=f(x)的解析式;
(2)求数列{an}的通项公式;
(3)设
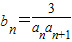 ,Tn是数列{bn}的前n项和,求使得
,Tn是数列{bn}的前n项和,求使得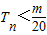 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
【答案】分析:(1)易得c=0,设这二次函数f(x)=ax2+bx(a≠0),根据导函数求得f(x)的表达式,
(2)根据点(n,Sn)(n∈N*)均在函数,y=f(x)的图象上,求出an的递推关系式,
(Ⅱ)把(1)题中an的递推关系式代入bn,根据裂项相消法求得Tn,最后解得使得得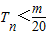 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
解答:解:(1)易得c=0,设二次函数f(x)=ax2+bx+c,则f'(x)=2ax+b.…(1分)
由于f'(x)=6x-2,得:a=3,b=-2…(2分)
所以f(x)=3x2-2x.…(3分)
(2)由点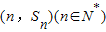 均在函数y=f(x)的图象上,又f(x)=3x2-2x,
均在函数y=f(x)的图象上,又f(x)=3x2-2x,
所以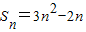 .…(4分)
.…(4分)
当n≥2时,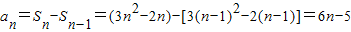 ;…(6分)
;…(6分)
当n=1时,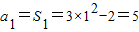 .…(7分)
.…(7分)
所以,an=6n-5(n∈N*)…(8分)
(3)由(2)得知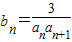 =
=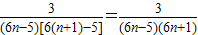 …(9分)
…(9分)
=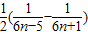 ,…(11分)
,…(11分)
故Tn=b1+b2+…+bn=
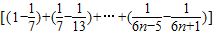
=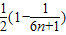 .…(12分)
.…(12分)
要使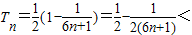 f(x)([1,e])成立,需要满足
f(x)([1,e])成立,需要满足 ≤a,…(13分)
≤a,…(13分)
即m≥10,所以满足要求的最小正整数m为10.…(14分)
点评:本题主要考查二次函数、等差数列、数列求和、不等式等基础知识和基本的运算技能,考查分析问题的能力和推理能力.
(2)根据点(n,Sn)(n∈N*)均在函数,y=f(x)的图象上,求出an的递推关系式,
(Ⅱ)把(1)题中an的递推关系式代入bn,根据裂项相消法求得Tn,最后解得使得得
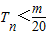 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.解答:解:(1)易得c=0,设二次函数f(x)=ax2+bx+c,则f'(x)=2ax+b.…(1分)
由于f'(x)=6x-2,得:a=3,b=-2…(2分)
所以f(x)=3x2-2x.…(3分)
(2)由点
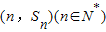 均在函数y=f(x)的图象上,又f(x)=3x2-2x,
均在函数y=f(x)的图象上,又f(x)=3x2-2x,所以
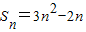 .…(4分)
.…(4分)当n≥2时,
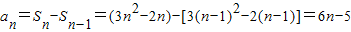 ;…(6分)
;…(6分)当n=1时,
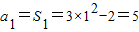 .…(7分)
.…(7分)所以,an=6n-5(n∈N*)…(8分)
(3)由(2)得知
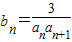 =
=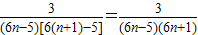 …(9分)
…(9分)=
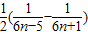 ,…(11分)
,…(11分)故Tn=b1+b2+…+bn=

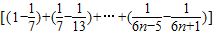
=
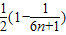 .…(12分)
.…(12分)要使
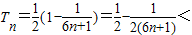 f(x)([1,e])成立,需要满足
f(x)([1,e])成立,需要满足 ≤a,…(13分)
≤a,…(13分)即m≥10,所以满足要求的最小正整数m为10.…(14分)
点评:本题主要考查二次函数、等差数列、数列求和、不等式等基础知识和基本的运算技能,考查分析问题的能力和推理能力.

练习册系列答案
相关题目
 已知二次函数y=f(x)的图象如图所示:
已知二次函数y=f(x)的图象如图所示: