题目内容
现给出如下命题：
（1）若某音叉发出的声波可用函数y=0.002sin800πt（t∈R+）描述，其中t的单位是秒，则该声波的频率是400赫兹；
（2）在△ABC中，若c2=a2+b2+ab，则
；
（3）从一个总体中随机抽取一个样本容量为10的样本：11，10，12，10，9，8，9，11，12，8，则该总体标准差的点估计值是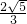
．
则其中正确命题的序号是
- A.（1）、（2）
- B.（1）、（3）
- C.（2）、（3）
- D.（1）、（2）、（3）
B
分析：（1）根据y=Asin（ωx+φ）中参数的物理意义求出函数的周期，进而可求频率；
（2）利用余弦定理表示出cosC，将已知的等式变形后代入，由C为三角形的内角，利用特殊角的三角函数值即可求出C的度数；
（3）先计算平均数，再计算该总体标准差的点估计值即可．
解答：（1）根据三角函数的模型有关定义可得：该声波的周期为T=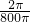
=
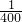，∴频率是f=
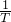=400赫兹，故（1）正确；
（2）∵c2=a2+b2+ab，即a2+b2-c2=-ab，∴由余弦定理得：cosC=-
，又∠C为三角形的内角，∴∠C=120°，故（2）不正确；
（3）这组数的平均数为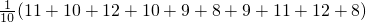
=10
∴该总体标准差的点估计值是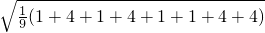
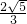=，故（3）正确．
综上知：（1）（3）正确
故选B．
点评：本题主要考查了y=Asin（ωx+φ）中参数的物理意义，考查了周期和频率；考查了余弦定理，以及特殊角的三角函数值，考查平均数与总体标准差的点估计值，属于中档题．
分析：（1）根据y=Asin（ωx+φ）中参数的物理意义求出函数的周期，进而可求频率；
（2）利用余弦定理表示出cosC，将已知的等式变形后代入，由C为三角形的内角，利用特殊角的三角函数值即可求出C的度数；
（3）先计算平均数，再计算该总体标准差的点估计值即可．
解答：（1）根据三角函数的模型有关定义可得：该声波的周期为T=
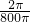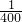=，∴频率是f=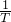=400赫兹，故（1）正确；（2）∵c2=a2+b2+ab，即a2+b2-c2=-ab，∴由余弦定理得：cosC=-
，又∠C为三角形的内角，∴∠C=120°，故（2）不正确；（3）这组数的平均数为
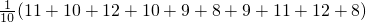=10∴该总体标准差的点估计值是
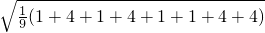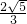=，故（3）正确．综上知：（1）（3）正确
故选B．
点评：本题主要考查了y=Asin（ωx+φ）中参数的物理意义，考查了周期和频率；考查了余弦定理，以及特殊角的三角函数值，考查平均数与总体标准差的点估计值，属于中档题．
练习册系列答案
相关题目
现给出如下命题：
（1）若直线l与平面α内无穷多条直线都垂直，则直线l⊥平面α；
（2）空间三点确定一个平面；
（3） 先后抛两枚硬币，用事件A表示“第一次抛出现正面向上”，用事件B表示“第二次抛出现反面向上”，则事件A和B相互独立且P（AB）=P(A)P(B)=
×
=
；
（4）样本数据-1，-1，0，1，1的标准差是1．
则其中正确命题的序号是（ ）
（1）若直线l与平面α内无穷多条直线都垂直，则直线l⊥平面α；
（2）空间三点确定一个平面；
（3） 先后抛两枚硬币，用事件A表示“第一次抛出现正面向上”，用事件B表示“第二次抛出现反面向上”，则事件A和B相互独立且P（AB）=P(A)P(B)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
（4）样本数据-1，-1，0，1，1的标准差是1．
则其中正确命题的序号是（ ）
| A、（1）、（4） |
| B、（1）、（3） |
| C、（2）、（3）、（4） |
| D、（3）、（4） |
现给出如下命题：
（1）若直线l与平面α内无穷多条直线都垂直，则直线l⊥平面α；
（2）已知z∈C，则|z2|=z2；
（3）某种乐器发出的声波可用函数y=0.001sin400πt（t∈R+）来描述，则该声波的频率是200赫兹；
（4）样本数据-1，-1，0，1，1的标准差是
．
则其中正确命题的序号是（ ）
（1）若直线l与平面α内无穷多条直线都垂直，则直线l⊥平面α；
（2）已知z∈C，则|z2|=z2；
（3）某种乐器发出的声波可用函数y=0.001sin400πt（t∈R+）来描述，则该声波的频率是200赫兹；
（4）样本数据-1，-1，0，1，1的标准差是
2
| ||
| 5 |
则其中正确命题的序号是（ ）
| A、（1）、（4） |
| B、（1）、（3） |
| C、（2）、（3）、（4） |
| D、（3）、（4） |