题目内容
20.已知等差数列(1)求![]() 的值;
的值;
(2)若![]() 与
与![]() 的等差中项为
的等差中项为![]() ,
,![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
本小题考查数列的概念,等差数列,等比数列,对数与指数互相转化等基础知识,考查综合运用数学知识解决问题的能力,
(Ⅰ)解法一:当n=1时,a1=S1=p-2+q,
当n≥2时,an=Sn-Sn-1=pn2-2n+q-p(n-1)2+2(n-1)-q
=2pn-p-2.
∵{an}是等差数列,
∴p-2+q=2p-p-2.
∴q=0.
解法二:当n=1时,a1=S1=p-2+q,
当n≥2时,an=Sn-Sn-1=pn2-2n+q-p(n-1)2+2(n-1)-q
=2pn-p-2.
当n≥3时,an-an-1=2pn-p-2-[2p(n-1)-p-2]=2p,
a2=p-2+q+2p=3p-2+q,
又a2=2p·2-P-2=3P-2,
所以3p-2+q=3p-2,得
q=0.
(Ⅱ)解:∵a3=![]() ,
,
∴a3=18.
又a3=6p-p-2,
∴6p-p-2=18.
∴p=4.
∴an=8n-6.
又an=2log2hn,得
bn=24a-3,
∴b1=2,![]() =24=16,即
=24=16,即
{bn}是等比数列.
所以数列{bn}的前n项和Tn=![]() (16n-1).
(16n-1).

练习册系列答案
相关题目
 的公差是
的公差是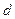 ,
, 是该数列的前
是该数列的前 项和.
项和. 表示
表示 ,其中
,其中 、
、
 ,求
,求 项的和分别为
项的和分别为
 ,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列
,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列 项和
项和 ,前
,前 项和
项和 ,求数列
,求数列 .”
.” 的前
的前 项和为
项和为 ,
,
 与前
与前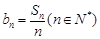 求证:数列
求证:数列 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列. 的前
的前 项和为
项和为 ,且满足
,且满足 ,则数列
,则数列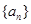 的前
的前 项和为
项和为 ,且
,且 ,
, .
. ,求证:数列
,求证:数列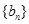 是等比数列,并求其前
是等比数列,并求其前