题目内容
 如图,在45°的二面角α-l-β的棱上有两点A、B,点C、D分别在α,β内,且AC⊥AB,∠ABD=45°,AC=AB=BD=1,则CD的长度为( )
如图,在45°的二面角α-l-β的棱上有两点A、B,点C、D分别在α,β内,且AC⊥AB,∠ABD=45°,AC=AB=BD=1,则CD的长度为( )分析:过D作DE垂直AB于E,由已知中二面角α-l-β为45°,且AC⊥AB,∠ABD=45°,AC=AB=BD=1,计算出DE,AE长后,代入异面直线上两点距离公式,可得答案.
解答:解:过D作DE垂直AB于E
∠ABD=45°,BD=1,
∴DE=
又∵AB=1
∴AE=1-
又∵二面角α-l-β为45°
故CD=
=
故选B
∠ABD=45°,BD=1,
∴DE=
| ||
| 2 |
又∵AB=1
∴AE=1-
| ||
| 2 |
又∵二面角α-l-β为45°
故CD=
| AC2+AE2+DE2-2AC•DE•COS45° |
2-
|
故选B
点评:本题考查的知识点是异面直线上两点之间的距离公式,其中计算出DE,AE长是解答本题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 (2013•广元二模)如图,在五面体EF-ABCD中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=l,AD=2
(2013•广元二模)如图,在五面体EF-ABCD中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=l,AD=2 (2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.
(2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.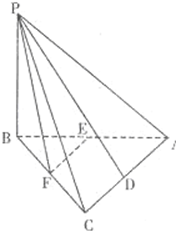 (2012•广安二模)如图,在三棱锥P-ABC中,PB⊥面ABC,∠ABC=90°,AB=BC=2,∠PAB=45°,点D,E,F分别是AC,AB,BC的中点.
(2012•广安二模)如图,在三棱锥P-ABC中,PB⊥面ABC,∠ABC=90°,AB=BC=2,∠PAB=45°,点D,E,F分别是AC,AB,BC的中点.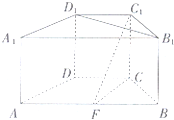 (2010•桂林二模)如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=2,BC=CD=1,AA1=1,F在棱AB(不含端点)上,且C1F与底面ABCD所成角的大小为45°
(2010•桂林二模)如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=2,BC=CD=1,AA1=1,F在棱AB(不含端点)上,且C1F与底面ABCD所成角的大小为45°
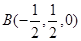 ,P(0,0,2).
,P(0,0,2).
 ,
, 于是
于是 ,所以
,所以
 设平面PCD的法向量
设平面PCD的法向量 ,
, ,即
,即 .不防设
.不防设 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量 于是
于是 从而
从而 .
. .
. ,由此得
,由此得 .
.
 ,解得
,解得 ,即
,即 .
. ,可得
,可得 ,又由
,又由 ,
, ,故
,故 .又
.又 ,所以
,所以
 于点H,连接DH.由
于点H,连接DH.由 ,可得
,可得 .
. ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在 中,
中, ,由此得
,由此得 由(1)知
由(1)知 ,故在
,故在 中,
中,
 所以二面角
所以二面角 的正弦值为
的正弦值为 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故 .在
.在 中,
中, 故
故

 中,由
中,由 ,
, ,
,
 .由余弦定理,
.由余弦定理, ,
,