题目内容
已知函数f（x）=lnx-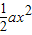
-2x．（Ⅰ）当a=3时，求函数f（x）的极大值；
（Ⅱ）若函数f（x）存在单调递减区间，求实数a的取值范围．
【答案】分析：（Ⅰ）当a=3时，利用导数求出单调区间，得出极值点，求得极值．
（Ⅱ）题意f′（x）＜0在（0，+∞）上有解，即ax2+2x-1＞0在（0，+∞）上有解．
解答：（Ⅰ）解：
，
．
由f′（x）＞0，得
，由f′（x）＜0，得
．
所以y=f（x）存在极大值
．
（Ⅱ）解：
，
依题意f′（x）＜0在（0，+∞）上有解，即ax2+2x-1＞0在（0，+∞）上有解．
当a≥0时，显然有解；
当a＜0时，由方程ax2+2x-1=0至少有一个正根，得-1＜a＜0； 所以a＞-1．
点评：本题考查函数导数与单调性的关系，函数极值，零点存在性定理．考查推理论证，运算求解能力．
（Ⅱ）题意f′（x）＜0在（0，+∞）上有解，即ax2+2x-1＞0在（0，+∞）上有解．
解答：（Ⅰ）解：
，．由f′（x）＞0，得
，由f′（x）＜0，得．所以y=f（x）存在极大值
．（Ⅱ）解：
，依题意f′（x）＜0在（0，+∞）上有解，即ax2+2x-1＞0在（0，+∞）上有解．
当a≥0时，显然有解；
当a＜0时，由方程ax2+2x-1=0至少有一个正根，得-1＜a＜0； 所以a＞-1．
点评：本题考查函数导数与单调性的关系，函数极值，零点存在性定理．考查推理论证，运算求解能力．
练习册系列答案
阅读快车系列答案
相关题目