题目内容
若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则a的取值范围是 .
-2<a≤2
解析:当a-2=0,即a=2时,不等式为-4<0恒成立,∴a=2.
当a-2≠0时,则a满足
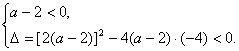
解得-2<a<2.
∴a的取值范围是-2<a≤2.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
题目内容
若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则a的取值范围是 .
-2<a≤2
解析:当a-2=0,即a=2时,不等式为-4<0恒成立,∴a=2.
当a-2≠0时,则a满足
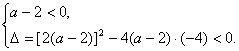
解得-2<a<2.
∴a的取值范围是-2<a≤2.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案