题目内容
已知函数f(x)=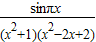 ,对于下列命题:
,对于下列命题:①函数f(x)是奇函数;
②直线x=
 是函数f(x)图象的对称轴;
是函数f(x)图象的对称轴;③对任意x∈R,f(x)满足|f(x)|<1;
④对任意x∈(-1,0),函数f(x)的导数满足f′(x)<0.
其中正确命题为 (写出命题序号即可).
【答案】分析:①根据函数的解析式求得函数的定义域,根据奇函数的定义,验证f(-x)=-f(x),可知该命题的正误;
②根据轴对称图形的定义,在函数f(x)图象上任取点P(x,y),求出点P关于直线x= 的对称点是P′(1-x,y),验证点P′在函数的图象上即可;
的对称点是P′(1-x,y),验证点P′在函数的图象上即可;
③根据二次函数的最值和不等式的基本性质,可以求出x2+1≥1;x2-2x+2=(x-1)2+1≥1,注意等号成立的条件,从而求得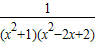 的范围,根据正弦函数的有界性,从而求得结论正确;
的范围,根据正弦函数的有界性,从而求得结论正确;
④对函数求导,求出f′( )<0,
)<0,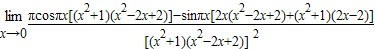 =2π>0,从而可知?x∈(-1,0),函数f(x)的导数满足f′(x)=0.可知该命题错误.
=2π>0,从而可知?x∈(-1,0),函数f(x)的导数满足f′(x)=0.可知该命题错误.
解答:解:①函数的定义域为R,f(-x)= =
=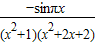 ≠-f(x)
≠-f(x)
∴函数f(x)不是奇函数故①错;
②在函数f(x)图象上任取点P(x,y),则点P关于直线x= 的对称点是P′(1-x,y)
的对称点是P′(1-x,y)
而f(1-x)=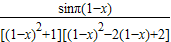 =
= =y
=y
∴直线x= 是函数f(x)图象的对称轴;故②正确;
是函数f(x)图象的对称轴;故②正确;
③∵x2+1≥1,当x=0时等号成立;x2-2x+2=(x-1)2+1≥1,当x=1时等号成立,
∴(x2+1)[(x-1)2+1]>1,∴0< <1,
<1,
而|sinπx|≤1,∴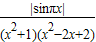 <1,即|f(x)|<1;故③正确;
<1,即|f(x)|<1;故③正确;
④f′(x)=
f′(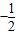 )=
)= <0,
<0,
而 =2π>0,
=2π>0,
?x∈(-1,0),函数f(x)的导数满足f′(x)=0.故④错
故正确命题为②③
故答案为:②③.
点评:本题考查函数的奇偶性的定义和对称性以及函数的值域的求法,导数的除法运算法则等知识,综合性强,考查灵活应用知识分析解决问题的能力,和运算能力,其中命题④计算量大,增加了试题的难度.属中档题.
②根据轴对称图形的定义,在函数f(x)图象上任取点P(x,y),求出点P关于直线x=
 的对称点是P′(1-x,y),验证点P′在函数的图象上即可;
的对称点是P′(1-x,y),验证点P′在函数的图象上即可;③根据二次函数的最值和不等式的基本性质,可以求出x2+1≥1;x2-2x+2=(x-1)2+1≥1,注意等号成立的条件,从而求得
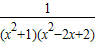 的范围,根据正弦函数的有界性,从而求得结论正确;
的范围,根据正弦函数的有界性,从而求得结论正确;④对函数求导,求出f′(
 )<0,
)<0,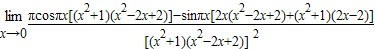 =2π>0,从而可知?x∈(-1,0),函数f(x)的导数满足f′(x)=0.可知该命题错误.
=2π>0,从而可知?x∈(-1,0),函数f(x)的导数满足f′(x)=0.可知该命题错误.解答:解:①函数的定义域为R,f(-x)=
 =
=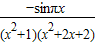 ≠-f(x)
≠-f(x)∴函数f(x)不是奇函数故①错;
②在函数f(x)图象上任取点P(x,y),则点P关于直线x=
 的对称点是P′(1-x,y)
的对称点是P′(1-x,y)而f(1-x)=
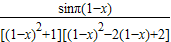 =
= =y
=y∴直线x=
 是函数f(x)图象的对称轴;故②正确;
是函数f(x)图象的对称轴;故②正确;③∵x2+1≥1,当x=0时等号成立;x2-2x+2=(x-1)2+1≥1,当x=1时等号成立,
∴(x2+1)[(x-1)2+1]>1,∴0<
 <1,
<1,而|sinπx|≤1,∴
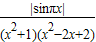 <1,即|f(x)|<1;故③正确;
<1,即|f(x)|<1;故③正确;④f′(x)=

f′(
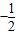 )=
)= <0,
<0,而
 =2π>0,
=2π>0,?x∈(-1,0),函数f(x)的导数满足f′(x)=0.故④错
故正确命题为②③
故答案为:②③.
点评:本题考查函数的奇偶性的定义和对称性以及函数的值域的求法,导数的除法运算法则等知识,综合性强,考查灵活应用知识分析解决问题的能力,和运算能力,其中命题④计算量大,增加了试题的难度.属中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|