题目内容
已知函数
．
（1）求函数定义域和函数图像所过的定点；
（2）若已知
时，函数最大值为2，求
的值．
（1）
，
；（2）
解析试题分析：（1）根据对数的真数大于0，可求得定义域，再根据
可求得所过定点。（2）根据的范围先求整体真数的范围，再根据对数的单调性求值域，得到最大值是其等于2，解出a。但这道题给的是
，所以需分两种情况讨论。
试题解析：（1）令
，解得
，故定义域为
令
，解得
，故函数过定点
（2）若
，函数
在上单调递增，
故
时
，解得；
若
，函数在上单调递减，
故
时
，解得
；
综上，。
考点：对数函数的定义域，定点和单调性
练习册系列答案
相关题目
（
）.
，求函数
的极值；
，不等式
恒成立，求实数
的取值范围.
，
的图象；
，函数
.
时，求
的最小值;
的范围，使得对于区间
上的任意三个实数
，都存在以
为边长的三角形.
R).
)上是增函数，求实数a的取值范围;
，且f(x0)=3，求x0的值；
，且在R上是减函数，求实数a的取值范围。
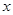（单位：元，
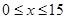）的关系是t=
.
在区间
上有最大值
，求实数
的值
上任取一点
，设点
轴上的正投影为点
．当点
满足
，动点
.
，若
、
是曲线
，求
的取值范围.
，恒过定点
．
；
的图象向下平移1个单位，再向左平移
，设函数
，直接写出
上的函数
，若在其定义域内，不等式
恒成立，求实数
的取值范围．