题目内容
已知定点F(2,0),直线l:x=2,点P为坐标平面上的动点,过点P作直线l的垂线,垂足为点Q,且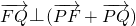 .设动点P的轨迹为曲线C.
.设动点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点F的直线l1与曲线C有两个不同的交点A、B,求证: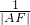 +
+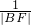 =
= ;
;
(3)记 与
与 的夹角为θ(O为坐标原点,A、B为(2)中的两点),求cosθ的取值范围.
的夹角为θ(O为坐标原点,A、B为(2)中的两点),求cosθ的取值范围.
(1)解:设点P的坐标为(x,y). (1分)
由题意,可得Q(-2,y),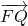 =(-4,y),
=(-4,y), =(2-x,-y),
=(2-x,-y), =(-2-x,0).(3分)
=(-2-x,0).(3分)
由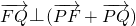 ,得
,得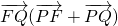 =0,即(-4,y)•(-2x,-y)=0
=0,即(-4,y)•(-2x,-y)=0
∴y2=8x(x≥0). (6分)
∴所求曲线C的方程为y2=8x(x≥0).
(2)证明:因为过点F的直线l1与曲线C有两个不同的交点A、B,所以l1的斜率不为零,
故设直线l1的方程为x=my+2. (7分)
于是A、B的坐标(x1,y1)、(x2,y2)为方程组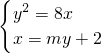 的实数解.
的实数解.
消x并整理得y2-8my-16=0. (8分)
于是y1+y2=8m,y1y2=-16,
∴x1+x2=8m2+4,x1x2=4,(10分)
又因为曲线y2=8x(x≥0)的准线为x=-2,
所以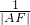 +
+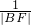 =
=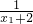 +
+ =
=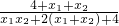 =
= ,得证. (12分)
,得证. (12分)
(3)解:由(2)可知, =(x1,y1),
=(x1,y1), =(x2,y2).
=(x2,y2).
∴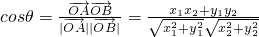 =
=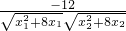 =
=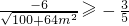 (当且仅当m=0时,等号成立). (16分)
(当且仅当m=0时,等号成立). (16分)
∴cosθ的取值范围为[- ,0). (18分)
,0). (18分)
分析:(1)确定向量的坐标,利用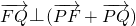 ,得
,得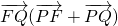 =0,由此可求曲线C的方程;
=0,由此可求曲线C的方程;
(2)设直线l1的方程为x=my+2与抛物线方程联立,利用韦达定理,结合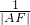 +
+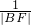 =
=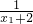 +
+ ,即可证得结论;
,即可证得结论;
(3)确定 =(x1,y1),
=(x1,y1), =(x2,y2),利用
=(x2,y2),利用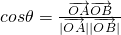 ,可求cosθ的取值范围.
,可求cosθ的取值范围.
点评:本题考查向量知识的运用,考查轨迹方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查计算能力,属于中档题.
由题意,可得Q(-2,y),
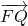 =(-4,y),
=(-4,y), =(2-x,-y),
=(2-x,-y), =(-2-x,0).(3分)
=(-2-x,0).(3分)由
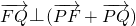 ,得
,得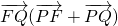 =0,即(-4,y)•(-2x,-y)=0
=0,即(-4,y)•(-2x,-y)=0∴y2=8x(x≥0). (6分)
∴所求曲线C的方程为y2=8x(x≥0).
(2)证明:因为过点F的直线l1与曲线C有两个不同的交点A、B,所以l1的斜率不为零,
故设直线l1的方程为x=my+2. (7分)
于是A、B的坐标(x1,y1)、(x2,y2)为方程组
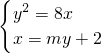 的实数解.
的实数解.消x并整理得y2-8my-16=0. (8分)
于是y1+y2=8m,y1y2=-16,
∴x1+x2=8m2+4,x1x2=4,(10分)
又因为曲线y2=8x(x≥0)的准线为x=-2,
所以
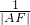 +
+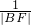 =
=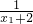 +
+ =
=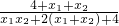 =
= ,得证. (12分)
,得证. (12分)(3)解:由(2)可知,
 =(x1,y1),
=(x1,y1), =(x2,y2).
=(x2,y2).∴
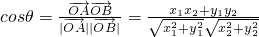 =
=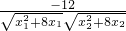 =
=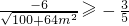 (当且仅当m=0时,等号成立). (16分)
(当且仅当m=0时,等号成立). (16分)∴cosθ的取值范围为[-
 ,0). (18分)
,0). (18分)分析:(1)确定向量的坐标,利用
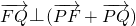 ,得
,得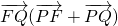 =0,由此可求曲线C的方程;
=0,由此可求曲线C的方程;(2)设直线l1的方程为x=my+2与抛物线方程联立,利用韦达定理,结合
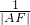 +
+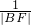 =
=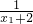 +
+ ,即可证得结论;
,即可证得结论;(3)确定
 =(x1,y1),
=(x1,y1), =(x2,y2),利用
=(x2,y2),利用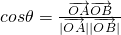 ,可求cosθ的取值范围.
,可求cosθ的取值范围.点评:本题考查向量知识的运用,考查轨迹方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查计算能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 已知定点F(2,0),动圆P经过点F且与直线x=-2相切,记动圆的圆心P的轨迹为C.
已知定点F(2,0),动圆P经过点F且与直线x=-2相切,记动圆的圆心P的轨迹为C.