题目内容
已知 ,( a为常数,e为自然对数的底).
,( a为常数,e为自然对数的底).
(1)
(2)
 时取得极小值,试确定a的取值范围;
时取得极小值,试确定a的取值范围;
(3)在(Ⅱ)的条件下,设 的极大值构成的函数
的极大值构成的函数 ,将a换元为x,试判断
,将a换元为x,试判断 是否能与
是否能与 (m为确定的常数)相切,并说明理由.
(m为确定的常数)相切,并说明理由.
解(1)当 时,
时, .
. .
.
所以 .
.
(2)
 .
.
令 ,得
,得 或
或 .
.
当 ,即
,即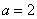 时,
时,
 恒成立,
恒成立,
此时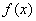 在区间
在区间 上单调递减,没有极小值;
上单调递减,没有极小值;
当 ,即
,即 时,
时,
若 ,则
,则 .若
.若 ,则
,则 .
.
所以 是函数
是函数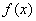 的极小值点.当
的极小值点.当 ,即
,即 时,
时,
若 ,则
,则 .若
.若 ,则
,则 .
.
此时 是函数
是函数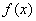 的极大值点.
的极大值点.
综上所述,使函数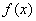 在
在 时取得极小值的
时取得极小值的 的取值范围是
的取值范围是 .
.
(3)由(Ⅱ)知当 ,且
,且 时,
时, ,
,
因此 是
是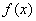 的极大值点,极大值为
的极大值点,极大值为 .
.
所以 .
.  .
.
令 .
.
则 恒成立,即
恒成立,即 在区间
在区间 上是增函数.
上是增函数.
所以当 时,
时, ,即恒有
,即恒有 .
.
又直线 的斜率为
的斜率为 ,
,
所以曲线 不能与直线
不能与直线 相切.
相切.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 中,得出的一般性结论是__________。
中,得出的一般性结论是__________。 在区间
在区间 上的最大值和最小值分别为 ( )
上的最大值和最小值分别为 ( ) B.
B.  C.
C.  D.
D. 
 ,则
,则 ____________.
____________. 的模为
的模为 ,则cos2a=( )
,则cos2a=( ) B.
B. C.
C. D.
D.
 ,a=10,则边长c的取值范围是( )
,a=10,则边长c的取值范围是( ) B.(10,+∞)
B.(10,+∞)
 在R是单调函数,则实数
在R是单调函数,则实数 的取值范围是( )
的取值范围是( ) B、
B、
 D、
D、
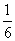 B.
B.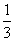 C.
C.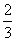 D.
D.