题目内容
3.设向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=1,\overrightarrow a•\overrightarrow b=0$,若向量$\overrightarrow c$满足$|{\vec c-\vec a-\vec b}|=1$,则$|{\overrightarrow c}|$的取值范围是( )| A. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | B. | [$\sqrt{2}$-1,$\sqrt{2}$+2] | C. | [1,$\sqrt{2}$+1] | D. | [1,$\sqrt{2}$+2]1 |
分析 由题意知,$\overrightarrow{a},\overrightarrow{b}$是互相垂直的两个单位向量,在平面直角坐标系中画出图形,由|$\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}$|=|$\overrightarrow{c}-(\overrightarrow{a}+\overrightarrow{b})$|=1,借助几何意义求得答案.
解答 解:∵$|{\overrightarrow a}|=|{\overrightarrow b}|=1,\overrightarrow a•\overrightarrow b=0$,且|$\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}$|=|$\overrightarrow{c}-(\overrightarrow{a}+\overrightarrow{b})$|=1,
∴作出图象如图,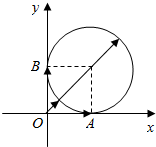
由图可知,$|{\overrightarrow c}|$最小值为$\sqrt{2}-1$,最大值为$\sqrt{2}+1$.
故选:A.
点评 本题考查平面向量的数量积运算,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
13.已知a,b均为正数,$\frac{1}{a}+\frac{4}{b}=3$,则使a+b≥c恒成立的c的取值范围是( )
| A. | (-∞,1] | B. | (-∞,2] | C. | (-∞,3] | D. | (-∞,9] |
12.不等式的log4x>$\frac{1}{2}$解集是( )
| A. | (2,+∞) | B. | (0,2) | C. | ($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$) |