题目内容
1.
已知半椭圆 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中 ,
, 是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
(1) 若三角形 是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
(2)若“果圆”方程为: ,
, 过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
(3) 若 是“果圆”上任意一点,求
是“果圆”上任意一点,求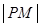 取得最小值时点
取得最小值时点 的横坐标.
的横坐标.

【答案】
(1) ,
,
(2)
(3)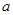 或
或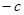
【解析】(I)∵
∴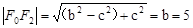 ,
,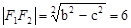 ,
,
于是,c2=16,a2=b2+c2=41,
所求“果圆”方程为 ,
,
(Ⅱ)①若直线l的斜率k存在,则由图可知,k2>3.设直线l的方程为:y=k(x-1),设点Q,N的坐标分别为(x1,y1),(x2,y2)
由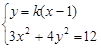 消x,得
消x,得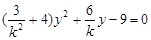
∴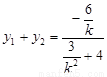 ,
,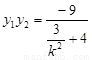
∴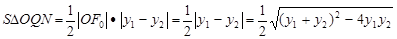
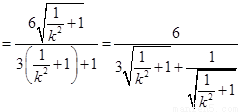
∵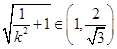 [来源:学*科*网]
[来源:学*科*网]
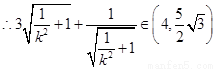
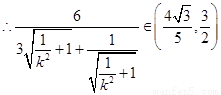
②若直线l⊥x轴,则︱QN︱=3,故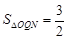
综上,得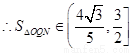
(3)设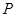 是“果圆”的半椭圆
是“果圆”的半椭圆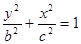
 上任意一点.设
上任意一点.设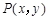 ,则
,则
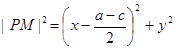
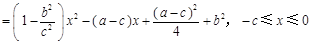 ,
,
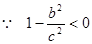 ,
,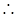
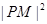 的最小值只能在
的最小值只能在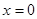 或
或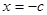 处取到.
处取到.
即当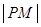 取得最小值时,
取得最小值时,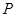 在点
在点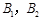 或
或 处.
处.
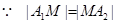 ,且
,且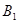 和
和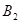 同时位于“果圆”的半椭圆
同时位于“果圆”的半椭圆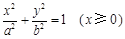 和半椭圆
和半椭圆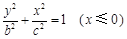 上
上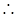 当
当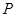 位于“果圆”的半椭圆
位于“果圆”的半椭圆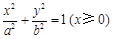 上时.
上时.
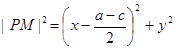 [来源:Zxxk.Com]
[来源:Zxxk.Com]
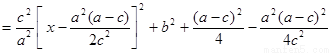 .
.
当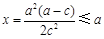 ,即
,即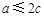 时,
时,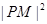 的最小值在
的最小值在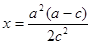 时取到,
时取到,
此时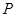 的横坐标是
的横坐标是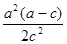 .
.
当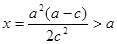 ,即
,即 时,由于
时,由于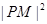 在
在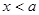 时是递减的,
时是递减的,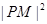 的最小值在
的最小值在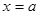 时取到,此时
时取到,此时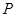 的横坐标是
的横坐标是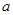 .
.
综上所述,若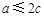 ,当
,当 取得最小值时,点
取得最小值时,点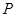 的横坐标是
的横坐标是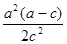 ;若
;若 ,当
,当 取得最小值时,点
取得最小值时,点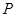 的横坐标是
的横坐标是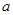 或
或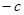 .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中 ,
, 是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点. 是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程; ,
, 过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围 是“果圆”上任意一点,求
是“果圆”上任意一点,求 取得最小值时点
取得最小值时点
 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中 。如图,设点
。如图,设点 ,
, ,
, 是相应椭圆的焦点,
是相应椭圆的焦点, ,
, 和
和 ,
, 是“果圆”
与
是“果圆”
与 ,
, 轴的交点,
轴的交点, 是边长为1的等边三角形,求“果圆”的方程;
是边长为1的等边三角形,求“果圆”的方程; ,求
,求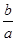 的取值范围;
的取值范围; ,使得斜率为
,使得斜率为 已知半椭圆
已知半椭圆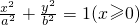 与半椭圆
与半椭圆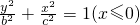 组成的曲线称为“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,设点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点,
组成的曲线称为“果圆”,其中a2=b2+c2,a>0,b>c>0.如图,设点F0,F1,F2是相应椭圆的焦点,A1,A2和B1,B2是“果圆”与x,y轴的交点, 的取值范围;
的取值范围;