题目内容
已知圆C:(x-3)2+(y-4)2=4,直线l1过定点A (1,0).
(Ⅰ)若l1与圆C相切,求l1的方程;
(Ⅱ)若l1与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时直线l1的方程.
(Ⅰ)若l1与圆C相切,求l1的方程;
(Ⅱ)若l1与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时直线l1的方程.
分析:(Ⅰ)通过直线l1的斜率存在与不存在两种情况,利用直线的方程与圆C相切,圆心到直线的距离等于半径,即可求l1的方程;
(Ⅱ)设直线方程为kx-y-k=0,求出圆心到直线的距离,弦长,得到三角形CPQ的面积的表达式,利用二次函数求出面积的最大值时的距离,然后求出直线的斜率,即可得到l1的直线方程.
(Ⅱ)设直线方程为kx-y-k=0,求出圆心到直线的距离,弦长,得到三角形CPQ的面积的表达式,利用二次函数求出面积的最大值时的距离,然后求出直线的斜率,即可得到l1的直线方程.
解答:解:(Ⅰ) ①若直线l1的斜率不存在,则直线l1:x=1,符合题意.
②若直线l1斜率存在,设直线l1的方程为y=k(x-1),即kx-y-k=0.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,
即:
=2,解之得 k=
.
所求直线l1的方程是x=1或3x-4y-3=0.
(Ⅱ)直线与圆相交,斜率必定存在,且不为0,设直线方程为kx-y-k=0,
则圆心到直l1的距离d=
又∵三角形CPQ面积S=
d×2
=d
=
∴当d=
时,S取得最小值2.
∴d=
=
,k=1或k=7.
∴直线方程为y=x-1,或y=7x-7.
②若直线l1斜率存在,设直线l1的方程为y=k(x-1),即kx-y-k=0.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,
即:
| |3k-4-k| | ||
|
| 3 |
| 4 |
所求直线l1的方程是x=1或3x-4y-3=0.
(Ⅱ)直线与圆相交,斜率必定存在,且不为0,设直线方程为kx-y-k=0,
则圆心到直l1的距离d=
| |2k-4| | ||
|
又∵三角形CPQ面积S=
| 1 |
| 2 |
| 4-d2 |
| 4-d2 |
| -(d2-2)2+4 |
∴当d=
| 2 |
∴d=
| |2k-4| | ||
|
| 2 |
∴直线方程为y=x-1,或y=7x-7.
点评:本题考查直线与圆的位置关系,考查直线与圆相切,考查三角形的面积的最值,考查计算能力,属于中档题.

练习册系列答案
相关题目
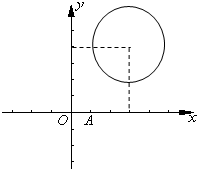 已知圆C:(x-3)2+(y-4)2=4,
已知圆C:(x-3)2+(y-4)2=4,