题目内容
已知函数f(x)=ex-ax,其中a>0。
(1)若对一切x∈R,f(x) ≥1恒成立,求a的取值集合;
(2)在函数f(x)的图像上去定点A(x1,f(x1)),B(x2,f(x2))(x1<x2),记直线AB的斜率为k,证明:存在x0∈(x1,x2),使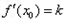 恒成立。
恒成立。
(1)若对一切x∈R,f(x) ≥1恒成立,求a的取值集合;
(2)在函数f(x)的图像上去定点A(x1,f(x1)),B(x2,f(x2))(x1<x2),记直线AB的斜率为k,证明:存在x0∈(x1,x2),使
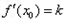 恒成立。
恒成立。解: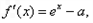
令
当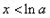 时
时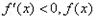 单调递减;
单调递减;
当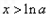 时
时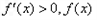 单调递增,
单调递增,
故当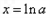 时,
时,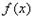 取最小值
取最小值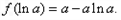
于是对一切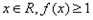 恒成立,
恒成立,
当且仅当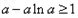 ①
①
令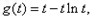 则
则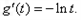
当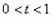 时,
时,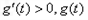 单调递增;
单调递增;
当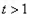 时,
时,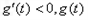 单调递减
单调递减
故当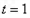 时,
时,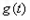 取最大值
取最大值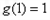
因此,当且仅当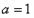 时,①式成立.综上所述,
时,①式成立.综上所述,
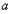 的取值集合为
的取值集合为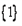 。
。
(Ⅱ)由题意知,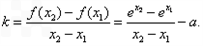
令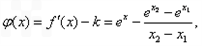
则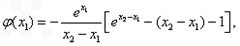
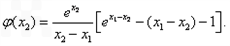
令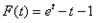 ,
,
则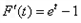 .当
.当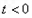 时,
时,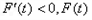 单调递减;
单调递减;
当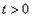 时,
时,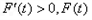 单调递增
单调递增
故当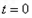 ,
,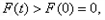
即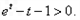 从而
从而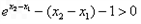 ,
,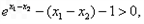
又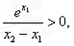
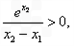
所以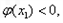
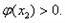
因为函数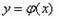 在区间
在区间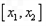 上的图像是连续不断的一条曲线,
上的图像是连续不断的一条曲线,
所以存在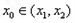 使
使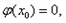 即
即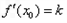 成立。
成立。
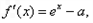
令

当
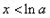 时
时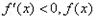 单调递减;
单调递减;当
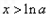 时
时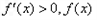 单调递增,
单调递增,故当
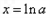 时,
时,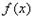 取最小值
取最小值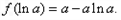
于是对一切
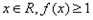 恒成立,
恒成立,当且仅当
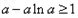 ①
①令
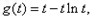 则
则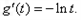
当
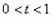 时,
时,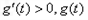 单调递增;
单调递增;当
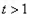 时,
时,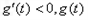 单调递减
单调递减故当
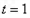 时,
时,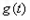 取最大值
取最大值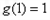
因此,当且仅当
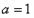 时,①式成立.综上所述,
时,①式成立.综上所述,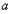 的取值集合为
的取值集合为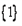 。
。(Ⅱ)由题意知,
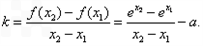
令
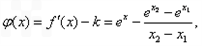
则
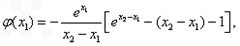
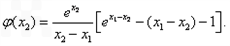
令
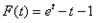 ,
,则
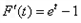 .当
.当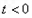 时,
时,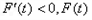 单调递减;
单调递减;当
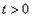 时,
时,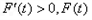 单调递增
单调递增故当
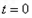 ,
,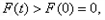
即
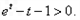 从而
从而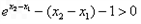 ,
,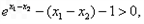
又
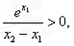
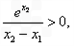
所以
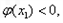
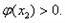
因为函数
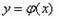 在区间
在区间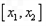 上的图像是连续不断的一条曲线,
上的图像是连续不断的一条曲线,所以存在
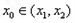 使
使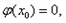 即
即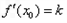 成立。
成立。
练习册系列答案
相关题目