题目内容
直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 的参数方程为
的参数方程为 (
( 为参数),
为参数), 为直线
为直线 与曲线
与曲线 的公共点. 以原点
的公共点. 以原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(Ⅰ)求点 的极坐标;
的极坐标;
(Ⅱ)将曲线 上所有点的纵坐标伸长为原来的
上所有点的纵坐标伸长为原来的 倍(横坐标不变)后得到曲线
倍(横坐标不变)后得到曲线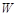 ,过点
,过点 作直线
作直线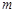 ,若直线
,若直线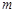 被曲线
被曲线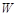 截得的线段长为
截得的线段长为 ,求直线
,求直线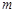 的极坐标方程.
的极坐标方程.
(Ⅰ)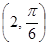 ;(Ⅱ)
;(Ⅱ)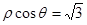 或
或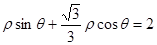 .
.
解析试题分析:(Ⅰ)把曲线 的参数方程化为的普通方程,将
的参数方程化为的普通方程,将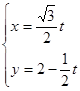 代入整理为关于
代入整理为关于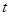 的二次方程,解出
的二次方程,解出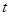 ,易得点
,易得点 的极坐标;(Ⅱ)通过坐标变换得出
的极坐标;(Ⅱ)通过坐标变换得出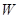 的普通方程,对直线
的普通方程,对直线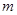 的斜率分类讨论,利用点到直线的距离公式求得
的斜率分类讨论,利用点到直线的距离公式求得 ,求出直线
,求出直线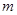 的普通方程,易得直线
的普通方程,易得直线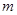 的极坐标方程.
的极坐标方程.
试题解析:(Ⅰ)曲线 的普通方程为
的普通方程为 ,将
,将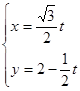 代人上式整理得
代人上式整理得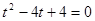 ,解得
,解得 .故点
.故点 的坐标为
的坐标为 ,其极坐标为
,其极坐标为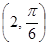 . 5分
. 5分
(Ⅱ)依题知,坐标变换式为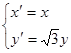 ,
,
故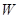 的方程为:
的方程为: ,即
,即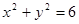 .
.
当直线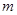 的斜率不存在时,其方程为
的斜率不存在时,其方程为 ,显然成立.
,显然成立.
当直线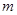 的斜率存在时,设其方程为
的斜率存在时,设其方程为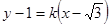 ,即
,即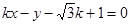 ,
,
则由已知,圆心 到直线
到直线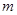 的距离为
的距离为 ,故
,故 ,
,
解得 .此时,直线
.此时,直线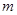 的方程为
的方程为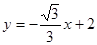 .
.
故直线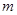 的极坐标方程为:
的极坐标方程为: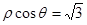 或
或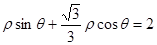 . 10分
. 10分
考点:直线、圆、椭圆的普通方程与参数方程的转化,直线的极坐标方程.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
 的直线与圆
的直线与圆 :
: 的一个交点为
的一个交点为 ,点
,点 为线段
为线段 的中点。
的中点。 .
. 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线 ,求|MA|·|MB|.
,求|MA|·|MB|. ,方向向量为
,方向向量为 的直线,圆方程
的直线,圆方程
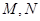 两点,求
两点,求 的值
的值 ,直线
,直线 的参数方程为
的参数方程为 ( t为参数,0≤
( t为参数,0≤ <
< ).
). 中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为
中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为 ,M,N分别为C与x轴,y轴的交点.
,M,N分别为C与x轴,y轴的交点. 中,圆
中,圆 的参数方程
的参数方程 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.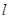 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 ,与直线
,与直线 ,求线段
,求线段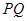 的长.
的长. 的方程为
的方程为 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数). 的普通方程;
的普通方程; 为曲线
为曲线 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.  轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线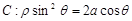
 ,过点
,过点 的直线
的直线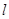 的参数方程为:
的参数方程为:
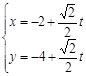 ,(t为参数),直线
,(t为参数),直线 分别交于
分别交于 两点.
两点.  成等比数列,求
成等比数列,求 的值.
的值.