题目内容
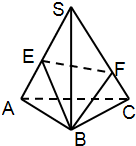 如图,S-ABC是正三棱锥且侧棱长为a,两侧棱SA,SC的夹角为30°,E,F分别是SA,SC上的动点,则三角形BEF的周长的最小值为( )
如图,S-ABC是正三棱锥且侧棱长为a,两侧棱SA,SC的夹角为30°,E,F分别是SA,SC上的动点,则三角形BEF的周长的最小值为( )分析:把正三棱锥沿SB剪开,并展开,形成三个全等的等腰三角形:△SBC、△SCA、△SAB′,连接BB′,交SC于F,交SA于E,则线段BB′就是△BEF的最小周长,易判断△B′SB为等腰直角三角形,由勾股定理可求BB′.
解答:解:把正三棱锥沿SB剪开,并展开,形成三个全等的等腰三角形:△SBC、△SCA、△SAB′,
则∠B′SA=∠BSC=∠ASC=30°,
连接BB′,交SC于F,交SA于E,则线段BB′就是△BEF的最小周长,
又SB=SB′=a,根据勾股定理,SB2+SB′2=BB′2=2a2,
所以BB′=
a,
故选A.
则∠B′SA=∠BSC=∠ASC=30°,
连接BB′,交SC于F,交SA于E,则线段BB′就是△BEF的最小周长,
又SB=SB′=a,根据勾股定理,SB2+SB′2=BB′2=2a2,
所以BB′=
| 2 |
故选A.
点评:本题考查了多面体表面上的距离问题及线线夹角求法问题,解题的关键是将多面体展开,将多面体表面上的轨迹长度问题变化为平面上的两点间距离问题研究,这里用到了几何中常用的降维的技巧,化体为面是一个重要的技巧.本题易因为没有把立体问题转化为平面问题研究而导致无法求解

练习册系列答案
相关题目
 如图,S是边长为a的正三角ABC所在平面外一点,SA=SB=SC=a,E、F是AB和SC的中点,则异面直线SA与EF所成的角为
如图,S是边长为a的正三角ABC所在平面外一点,SA=SB=SC=a,E、F是AB和SC的中点,则异面直线SA与EF所成的角为 如图,S-ABC是正三棱锥且侧棱长为a,E,F分别是SA,SC上的动点,三角形BEF的周长的最小值为
如图,S-ABC是正三棱锥且侧棱长为a,E,F分别是SA,SC上的动点,三角形BEF的周长的最小值为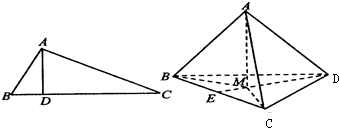 如图,在△ABC中,AB⊥AC,若AD⊥BC,则AB2=BD•BC;类似地有命题:在三棱锥A-BCD中,AD⊥面ABC,若A点在BCD内的射影为M,则有
如图,在△ABC中,AB⊥AC,若AD⊥BC,则AB2=BD•BC;类似地有命题:在三棱锥A-BCD中,AD⊥面ABC,若A点在BCD内的射影为M,则有 如图,S-ABC是正三棱锥且侧棱长为a,E,F分别是SA,SC上的动点,三角形BEF的周长的最小值为
如图,S-ABC是正三棱锥且侧棱长为a,E,F分别是SA,SC上的动点,三角形BEF的周长的最小值为 ,则侧棱SA,SC的夹角为
,则侧棱SA,SC的夹角为