题目内容
(10分)设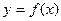 是定义在R上的偶函数,其图象关于
是定义在R上的偶函数,其图象关于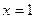 对称,对任意的
对称,对任意的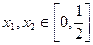 ,都有
,都有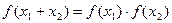 ,且
,且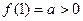
(1)求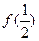 ;
;
(2)证明: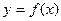 是周期函数。
是周期函数。
解:(1)因为对任意的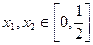 ,都有
,都有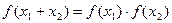
所以
又因为
所以
(2)因为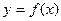 是定义在R上的偶函数,其图象关于
是定义在R上的偶函数,其图象关于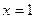 对称
对称
所以
即 ,
,
所以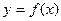 是周期为2的周期函数。
是周期为2的周期函数。
解析

练习册系列答案
相关题目
若函数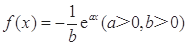 的图象在
的图象在 处的切线与圆
处的切线与圆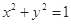 相切,则
相切,则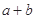 的最大值是( )
的最大值是( )
| A.4 | B.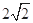 | C.2 | D.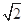 |
题目内容
(10分)设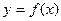 是定义在R上的偶函数,其图象关于
是定义在R上的偶函数,其图象关于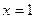 对称,对任意的
对称,对任意的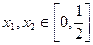 ,都有
,都有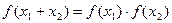 ,且
,且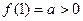
(1)求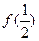 ;
;
(2)证明: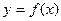 是周期函数。
是周期函数。
解:(1)因为对任意的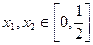 ,都有
,都有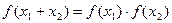
所以
又因为
所以
(2)因为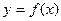 是定义在R上的偶函数,其图象关于
是定义在R上的偶函数,其图象关于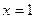 对称
对称
所以
即 ,
,
所以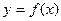 是周期为2的周期函数。
是周期为2的周期函数。
解析

若函数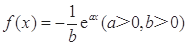 的图象在
的图象在 处的切线与圆
处的切线与圆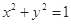 相切,则
相切,则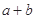 的最大值是( )
的最大值是( )
| A.4 | B.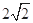 | C.2 | D.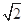 |