题目内容
若 和
和 都是定义在
都是定义在 上的函数,则“
上的函数,则“ 与
与 同是奇函数或偶函数”是“
同是奇函数或偶函数”是“ 是偶函数”的( )
是偶函数”的( )
A.充分非必要条件. B.必要非充分条件.
C.充要条件. D.既非充分又非必要条件
【答案】
A
【解析】
试题分析:显然当 与
与 同是奇函数或偶函数可以得出
同是奇函数或偶函数可以得出 是偶函数,而当
是偶函数,而当 是偶函数时,不妨令
是偶函数时,不妨令 ,此时
,此时
 为偶函数,
为偶函数, 为偶函数
为偶函数 为奇函数,故“
为奇函数,故“ 与
与 同是奇函数或偶函数”是“
同是奇函数或偶函数”是“ 是偶函数”的充分非必要条件,答案选A.
是偶函数”的充分非必要条件,答案选A.
考点:导数的几何意义.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 和
和 都是定义在
都是定义在 上的函数,则“
上的函数,则“ 是偶函数”的( )
是偶函数”的( ) 都是定义在
都是定义在 上的函数,
上的函数, ,
, ,
, ,
, ,在有穷数列
,在有穷数列 中,任意取正整数
中,任意取正整数 ,则前
,则前 项和大于
项和大于 的概率是 ( )
的概率是 ( ) B.
B. C.
C. D.
D.
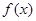 和
和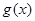 都是定义在
都是定义在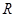 上的奇函数,设
上的奇函数,设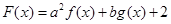 ,若
,若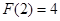 ,则
,则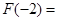 .
.