Question

设x，y满足约束条件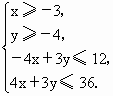

(1)求目标函数z=2x＋3y的最小值与最大值；

(2)求目标函数z=－4x＋3y－24的最小值与最大值．

Answer 1

答案：-18,38;-84,-12
解析：

(1)作出可行域(如图阴影部分)． 解：令z=0，作直线l：2x＋3y=0． 仿前，当把直线l向下平移时，所对应的z=2x＋3y的函数值随之减小，所以，直线经过可行域的顶点B时，z=2x＋3y取得最小值． 从图中可以看出，顶点B是直线x=－3与直线y=－4的交点，其坐标为(－3，－4)； 当把l向上平移时，所对应的z=2x＋3y的函数值随之增大，所以直线经过可行域的顶点D时，z=2x＋3y取得最大值． 顶点D是直线－4x＋3y=12与直线4x＋3y=36的交点，解方程组可以求得顶点D的坐标为(3，8)． 此时，顶点B(－3，－4)与顶点D(3，8)为最优解． 所以，． (2)可行域同(1)(如图阴影部分)． 作直线，仿前，把直线向下平移时，所对应的的函数值随之减小，即z=－4x＋3y－24的函数值随之减小，从图中可以看出，直线经过可行域顶点C时，取得最小值，即z=－4x＋3y－24取得最小值． 顶点C是直线4x＋3y=36与直线y=－4的交点，解方程组得到顶点C的坐标(12，－4)，代入目标函数z=－4x＋3y－24，得 ． 由于直线平行于直线－4x＋3y=12，因此当把直线向上平移到时，与可行域的交点不止一个，而是线段AD上的所有点．此时，．