Question

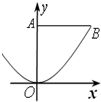（2013•怀化三模）如图，区域OAB由y轴，直线y=1及曲线y=x²（x≥0）围成，假设随机向该区域内投点，该点落在区域内每个位置是等可能的．现随机向区域投一点p，则直线OP的斜率小于1的概率是（　　）

• A．

  1

  5

• B．

  1

  4

• C．

  1

  3

• D．

  1

  2

Answer 1

分析：利用定积分分别确定区域的面积与坐标原点与该点的连线的斜率小于1的时区域的面积，即可求得概率．

解答：解：由题意，由y轴，直线y=1及曲线y=x²（x≥0）围成区域的面积为：
1-

∫

1 0

（x²）dx=1-

1

3

x³

|

1 0

=

2

3

又直线op的斜率小于1的区域内的面积为

2

3

-

1

2

=

1

6

，
则直线op的斜率小于1的概率是

1 6

2 3

=

1

4

．
故选B．

点评：本题考查几何概型，考查定积分知识的运用，解题的关键是利用定积分求面积．