Question

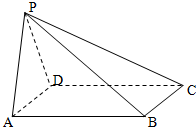如图，四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD．AB=2，PA=PD=3；
（1）求异面直线DC与PB所成的角的余弦值；
（2）求直线PB和平面ABCD所成角的正弦值．
（3）求二面角P-AB-C的余弦值．

Answer 1

分析：（1）以M点为坐标原点，建立空间坐标系，分别求出异面直线DC与PB的方向向量，代入向量夹角公式，可得答案；
（2）分别直线PB的方向向量和平面ABCD的法向量，代入向量夹角公式，可得答案；
（3）分别求出平面PAB和平面ABC的法向量，代入向量夹角公式，可得二面角P-AB-C的余弦值．

解答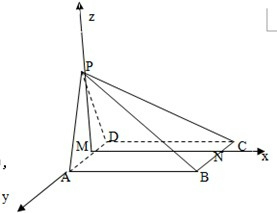：解：取AD，BC的中点M，N，连接PM，MN，
∵PA=PD，
∴PM⊥AD，
又∵平面PAD⊥平面AC
∴PM⊥平面AC
又∵MN?平面AC
∴PM⊥MN，
又∵MN⊥AD
故以M点为原点建立如图所示的坐标系，由AB=2，PA=PD=3得：
M（0，0，0），A（0，1，0），B（2，1，0），C（2，-1，0），D（0，-1，0），P（0，0，2

2

）
（1）直线PB的方向向量为

PB

=（2，1，2

2

），直线DC的方向向量为

DC

=（2，0，0）
设直线PB与直线DC所成的角为θ，则
cosθ=

| PB • DC |

| PB |•| DC |

=

4

2 13

=

2 13

13

所以，异面直线DC与PB所成的角的余弦值为

2 13

13

（2）由PM⊥平面AC，故平面AC的一个法向量为

MP

=（0，0，2

2

），直线PB的方向向量为

PB

=（2，1，2

2

），
设直线PB和平面ABCD所成角为α
则sinα=

| MP • PB |

| MP |•| PB |

=

8

2 2 • 13

=

2 26

13

所以，直线PB和平面ABCD所成角的正弦值为

2 26

13

（3）设平面PAB的一个法向量为

n

=（x，y，1）则

n

⊥

PB

，

n

⊥

AB

，且

AB

=（2，0，0），

PB

=（2，1，2

2

），
故

n • PB =0 n • AB =0

，即

2x+y-2 2 =0 2x=0

解得：x=0，y=2

2

∴

n

=（0，2

2

，1）
设二面角P-AB-C的平面角为β，
则cosβ=

| n • PM |

| n |•| PM |

=

1

3

故二面角P-AB-C的余弦值为

1

3

点评：本题考查的知识点是二面角的平面角及求法，异面直线及其所成的角，直线与平面所成的角，其中建立空间坐标系，将空间线面夹角转化为向量夹角是解答的关键．