题目内容
已知数列{an}的前n项和Sn满足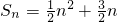 (n∈N*).
(n∈N*).
(1)求数列{an}的通项公式an;
(2)令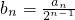 求数列{bn}的前n项和Tn
求数列{bn}的前n项和Tn
(3)令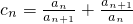 证明:2n<c1+c2+…
证明:2n<c1+c2+…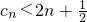 .
.
解:(1)n≥2时, =n+1
=n+1
n=1时,a1=S1=2,也满足上式
∴an=n+1(n∈N*).
(2)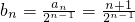
∴Tn=b1+b2+…+bn=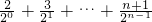 ①
①
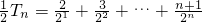 ②
②
①-②得
∴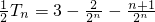
∴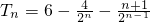
(3)∵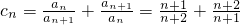 =
=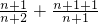 =
=
∴2n<c1+c2+…+cn,
∵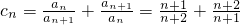 =
=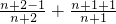 =
=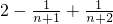
∴c1+c2+…+cn=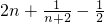
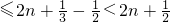
∴2n<c1+c2+…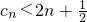 .
.
分析:(1)根据数列{an}的前n项和Sn满足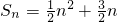 (n∈N*),利用n≥2时,an=Sn-Sn-1,结合n=1时,a1=S1=2,可求数列
(n∈N*),利用n≥2时,an=Sn-Sn-1,结合n=1时,a1=S1=2,可求数列 的通项公式an;
的通项公式an;
(2)根据数列{bn}通项的特点,利用错位相减法,可求数列{bn}的前n项和Tn
(3)根据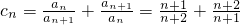 =
=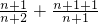 =
= ,可证不等式的左边;根据
,可证不等式的左边;根据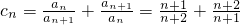 =
=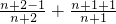 =
=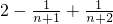 ,可证不等式的右边.
,可证不等式的右边.
点评:本题考查的重点是数列与不等式的综合,解题的关键是根据数列{an}的前n项和Sn满足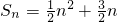 (n∈N*),利用n≥2时,an=Sn-Sn-1,利用错位相减法求数列的和,注意不等式证明中的适当放缩.
(n∈N*),利用n≥2时,an=Sn-Sn-1,利用错位相减法求数列的和,注意不等式证明中的适当放缩.
 =n+1
=n+1n=1时,a1=S1=2,也满足上式
∴an=n+1(n∈N*).
(2)
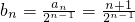
∴Tn=b1+b2+…+bn=
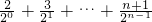 ①
①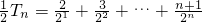 ②
②①-②得

∴
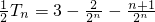
∴
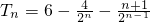
(3)∵
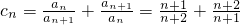 =
=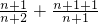 =
=
∴2n<c1+c2+…+cn,
∵
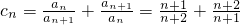 =
=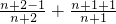 =
=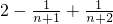
∴c1+c2+…+cn=
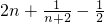
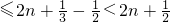
∴2n<c1+c2+…
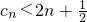 .
.分析:(1)根据数列{an}的前n项和Sn满足
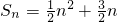 (n∈N*),利用n≥2时,an=Sn-Sn-1,结合n=1时,a1=S1=2,可求数列
(n∈N*),利用n≥2时,an=Sn-Sn-1,结合n=1时,a1=S1=2,可求数列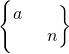 的通项公式an;
的通项公式an;(2)根据数列{bn}通项的特点,利用错位相减法,可求数列{bn}的前n项和Tn
(3)根据
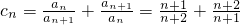 =
=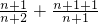 =
= ,可证不等式的左边;根据
,可证不等式的左边;根据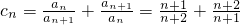 =
=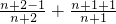 =
=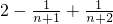 ,可证不等式的右边.
,可证不等式的右边.点评:本题考查的重点是数列与不等式的综合,解题的关键是根据数列{an}的前n项和Sn满足
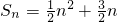 (n∈N*),利用n≥2时,an=Sn-Sn-1,利用错位相减法求数列的和,注意不等式证明中的适当放缩.
(n∈N*),利用n≥2时,an=Sn-Sn-1,利用错位相减法求数列的和,注意不等式证明中的适当放缩. 
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |