题目内容
在正方体ABCD-A1B1C1D1中,M,N分别为棱AA1和BB1的中点,则sin〈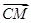 ,
,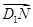 〉的值为 ( ).
〉的值为 ( ).
A.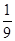 | B.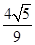 | C.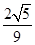 | D.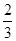 |
B
解析试题分析:设正方体棱长为2,以D为坐标原点,DA为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
则C(0,2,0),M(2,0,1),D1(0,0,2),N(2,2,1),可知 =(2,-2,1),
=(2,-2,1), =(2,2,-1),∴
=(2,2,-1),∴ •
• =2×2?2×2?1×1=?1,|
=2×2?2×2?1×1=?1,| | = 3, |
| = 3, |  |=3;∴cos<
|=3;∴cos< ,
, >=
>= ,所以sin<
,所以sin< ,
, >=
>=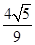 .故选B .
.故选B .
考点:用空间向量求平面间的夹角.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知 ,
, ,
, ,三角形
,三角形 的面积为( )
的面积为( )
A. | B.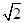 | C. | D. |
已知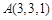 ,
,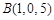 ,则下面说法中,正确的个数是 ( )
,则下面说法中,正确的个数是 ( )
(1)线段AB的中点坐标为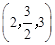 ;(2)线段AB的长度为
;(2)线段AB的长度为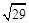 ;
;
(3)到A,B两点的距离相等的点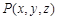 的坐标
的坐标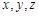 满足
满足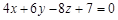 .
.
| A.0个 | B.1个 | C.2个 | D.3个 |
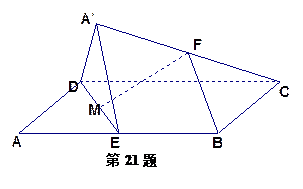
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成二面角的余弦值为( )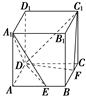
A.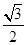 | B.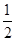 | C.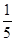 | D.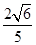 |
已知向量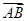 =(2,4,5),
=(2,4,5), =(3,x,y),若
=(3,x,y),若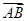 ∥
∥ ,则( )
,则( )
| A.x=6,y=15 | B.x=3,y= |
| C.x=3,y=15 | D.x=6,y= |
若两点的坐标是A(3cosα,3sinα,1),B(2cosβ,2sinβ,1),则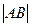 的取值范围是( )
的取值范围是( )
| A.[0,5] |
| B.[1,25] |
| C.(0,5) |
| D.[1,5] |
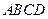 中,
中,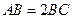 ,
,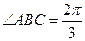 ,
,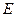 为线段
为线段 的中线,将△
的中线,将△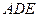 沿
沿 直线
直线 翻折成△
翻折成△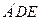 ,使平面
,使平面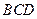 ,
,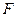 为线
为线 段
段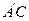 的中点.
的中点. ∥平面
∥平面 为线段
为线段 与平面
与平面