题目内容
过点C(0,1)的椭圆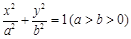 的离心率为
的离心率为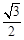 ,椭圆与x轴交于两点
,椭圆与x轴交于两点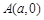 、
、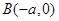 ,过点C的直线
,过点C的直线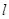 与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
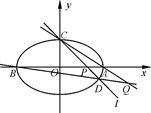
(I)当直线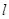 过椭圆右焦点时,求线段CD的长;
过椭圆右焦点时,求线段CD的长;
(II)当点P异于点B时,求证: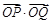 为定值.
为定值.
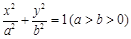 的离心率为
的离心率为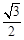 ,椭圆与x轴交于两点
,椭圆与x轴交于两点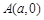 、
、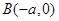 ,过点C的直线
,过点C的直线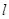 与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
(I)当直线
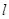 过椭圆右焦点时,求线段CD的长;
过椭圆右焦点时,求线段CD的长;(II)当点P异于点B时,求证:
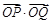 为定值.
为定值.(I) (II)
(II)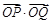 =4
=4
 (II)
(II)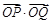 =4
=4试题分析:(Ⅰ)由已知得
 ,解得
,解得 ,所以椭圆方程为
,所以椭圆方程为 .
. 椭圆的右焦点为
 ,此时直线
,此时直线 的方程为
的方程为  ,代入椭圆方程得
,代入椭圆方程得 ,解得
,解得 ,代入直线
,代入直线 的方程得
的方程得  ,所以
,所以  ,故
,故 .
. (Ⅱ)当直线
 与
与 轴垂直时与题意不符.
轴垂直时与题意不符.设直线
 的方程为
的方程为 .代入椭圆方程得
.代入椭圆方程得 .
.解得
 ,代入直线
,代入直线 的方程得
的方程得 ,
,所以D点的坐标为
 .
.又直线AC的方程为
 ,又直线BD的方程为
,又直线BD的方程为 ,联立得
,联立得 因此
因此 ,又
,又 .所以
.所以 .故
.故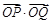 为定值.
为定值. 点评:本题主要考察了由椭圆的性质求解椭圆方程,直线与曲线相交的弦长公式的应用及向量的数量积的坐标表示的应用,属于圆锥曲线问题的综合应用

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
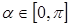 ,则方程
,则方程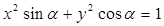 不能表示的曲线为( )
不能表示的曲线为( )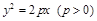 的焦点为
的焦点为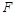 ,
,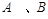 在抛物线上,且
在抛物线上,且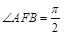 ,弦
,弦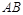 的中点
的中点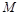 在其准线上的射影为
在其准线上的射影为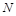 ,则
,则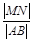 的最大值为________。
的最大值为________。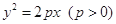 的焦点为
的焦点为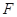 ,
,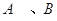 在抛物线上,且
在抛物线上,且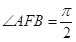 ,弦
,弦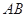 的中点
的中点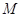 在其准线上的射影为
在其准线上的射影为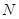 ,则
,则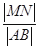 的最大值为
的最大值为
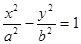 与
与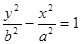 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为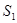 ,连接其四个焦点组成的四边形的面积为
,连接其四个焦点组成的四边形的面积为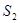 ,则
,则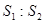 的最大值是
的最大值是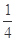
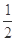
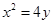 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆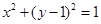 于点A、B、C、D,则
于点A、B、C、D,则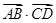 的值是________
的值是________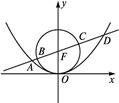
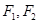 是椭圆
是椭圆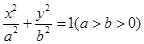 的左、右焦点,
的左、右焦点,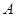 是椭圆上位于第一象限内的一点,点
是椭圆上位于第一象限内的一点,点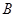 也在椭圆上,且满足
也在椭圆上,且满足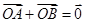 (
(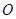 是坐标原点),
是坐标原点),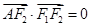 ,若椭圆的离心率为
,若椭圆的离心率为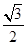 .
.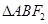 的面积等于
的面积等于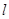 与(1)中的椭圆相交于不同的两点
与(1)中的椭圆相交于不同的两点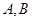 ,已知点
,已知点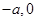 ),点
),点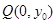 在线段
在线段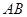 的垂直平分线上,且
的垂直平分线上,且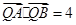 ,求
,求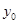 的值.
的值. ,焦距的一半为3的椭圆的标准方程是( )
,焦距的一半为3的椭圆的标准方程是( )



 =1的两条渐近线互相垂直,那么该双曲线的离心率是 .
=1的两条渐近线互相垂直,那么该双曲线的离心率是 .