题目内容
命题：“已知a、b、c、d是实数，若a=b，c=d，则a+c=b+d”.写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假.
解：逆命题:“已知a、b、c、d为实数，若a+c＝b+d，则a=b,c=d（即a与b、c与d均相等）.”
否命题:“已知a、b、c、d是实数，若a与b、c与d不都相等，则a+c≠b+d.”
逆否命题：“已知a、b、c、d是实数，若a+c≠b+d，则a与b、c与d不都相等.”
原命题为真命题.
若令a=3,b=2,c=1,d=2,则a+c=1+3=4,b+d=2+2=4,即a+c=b+d,但a≠b,c≠d,所以逆命题为假命题.
根据原命题与逆否命题、逆命题与否命题等价的性质,所以逆否命题为真命题、否命题为假命题.
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
命题：“已知a，b，c，d∈R，若a=b，c=d，则a+c=b+d”的逆否命题是：
已知a，b，c，d∈R，若a+c≠b+d，则a≠b或c≠d
已知a，b，c，d∈R，若a+c≠b+d，则a≠b或c≠d
．
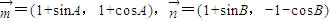，则
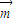与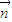
的夹角是锐角．则（ ）
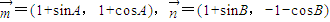，则
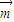与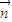
的夹角是锐角．则（ ）