题目内容
已知z1、z2是非零复数,且|z1+z2|=|z1-z2|,求证:
分析:只要证明![]() 为纯虚数即可.
为纯虚数即可.
证法一:设复数z1=a+bi,z2=c+di(a、b、c、d∈R),?
由|z1+z2|=|z1-z2|,?
得(a-c)2+(b-d)2=(a+c)2+(b+d)2,?
整理得ac+bd=0,?
而![]() [(ac+bd)+(bc-ad)i],?
[(ac+bd)+(bc-ad)i],?
由ac+bd=0,得![]() 为纯虚数得证.
为纯虚数得证.
证法二:设![]() =a+bi(a、b∈R),?
=a+bi(a、b∈R),?
则z1=z2(a+bi),∴|z1+z2|=|z2||(1+a)+bi|,?
|z1-z2|=|z2||(1-a)+bi|,?
代入|z1+z2|=|z1-z2|,得?
(1+a)2=(1-a)2,?
∴a=0.∴![]() 为纯虚数.
为纯虚数.
证法三:由|z1+z2|2=|z1-z2|2,?
得(z1+z2)(![]() )=(z1-z2)(
)=(z1-z2)(![]() ),?
),?
∴z1![]() +z2
+z2![]() =-z1
=-z1![]() -z2
-z2![]() ,?
,?
得z1![]() =-z2
=-z2![]() ,?
,?
∴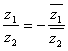 且
且![]() ≠0.∴
≠0.∴![]() 为纯虚数.
为纯虚数.
证法四:由|z1+z2|=|z1-z2|得|![]() +1|=|
+1|=|![]() -1|,?
-1|,?
由几何意义知![]() 对应的复数在虚轴上,?
对应的复数在虚轴上,?
∴![]() 为纯虚数.
为纯虚数.
证法五:设z1、z2、z1+z2在复平面对应的点分别为Z1、Z2、Z3,则四边形OZ1Z2Z3为平行四边形,?
再由|z1+z2|=|z1-z2|知平行四边形为矩形.?
∴OZ1⊥OZ2.∴![]() =ki(k∈R且k≠0).∴
=ki(k∈R且k≠0).∴![]() 为纯虚数.
为纯虚数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目