题目内容
6、在圆中有结论“如图,AB是圆O的直径,直线AC,BD是圆O过A、B的切线,P是圆O上任意一点,CD是过P的切线,则有PO2=PC•PD.”类比到椭圆:“AB是椭圆的长轴,O是椭圆中的中心,F1,F2是椭圆的焦点,直线AC,BD是椭圆过A、B的切线,P是椭圆上任意一点,CD是过P的切线,则有

PF1•PF2=PC•PD
.
分析:类比圆的半径和椭圆的焦半径,不难发现关系:OP2和PF1•PF2具有等价性.
解答:解:由题意可知:圆的半径和椭圆的焦半径,是类比对象,
不难发现关系:OP2和PF1•PF2具有等价性.
在圆中有PO2=PC•PD.则椭圆中PF1•PF2=PC•PD
故答案为:PF1•PF2=PC•PD
不难发现关系:OP2和PF1•PF2具有等价性.
在圆中有PO2=PC•PD.则椭圆中PF1•PF2=PC•PD
故答案为:PF1•PF2=PC•PD
点评:类比推理是一个难点,不易掌握,需要找到类比对象,本题是中档题.

练习册系列答案
相关题目
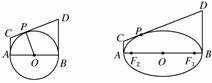
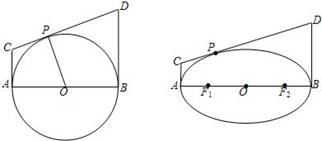
 在圆中有结论“如图,AB是圆O的直径,直线AC,BD是圆O过A、B的切线,P是圆O上任意一点,CD是过P的切线,则有PO2=PC•PD.”类比到椭圆:“AB是椭圆的长轴,O是椭圆中的中心,F1,F2是椭圆的焦点,直线AC,BD是椭圆过A、B的切线,P是椭圆上任意一点,CD是过P的切线,则有 .
在圆中有结论“如图,AB是圆O的直径,直线AC,BD是圆O过A、B的切线,P是圆O上任意一点,CD是过P的切线,则有PO2=PC•PD.”类比到椭圆:“AB是椭圆的长轴,O是椭圆中的中心,F1,F2是椭圆的焦点,直线AC,BD是椭圆过A、B的切线,P是椭圆上任意一点,CD是过P的切线,则有 . 在圆中有结论“如图,AB是圆O的直径,直线AC,BD是圆O过A、B的切线,P是圆O上任意一点,CD是过P的切线,则有PO2=PC•PD.”类比到椭圆:“AB是椭圆的长轴,O是椭圆中的中心,F1,F2是椭圆的焦点,直线AC,BD是椭圆过A、B的切线,P是椭圆上任意一点,CD是过P的切线,则有 .
在圆中有结论“如图,AB是圆O的直径,直线AC,BD是圆O过A、B的切线,P是圆O上任意一点,CD是过P的切线,则有PO2=PC•PD.”类比到椭圆:“AB是椭圆的长轴,O是椭圆中的中心,F1,F2是椭圆的焦点,直线AC,BD是椭圆过A、B的切线,P是椭圆上任意一点,CD是过P的切线,则有 .