题目内容
设奇函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0,则不等式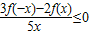 的解集为( )
的解集为( )A.(-∞,-2]∪(0,2]
B.[-2,0]∪[2,+∞)
C.(-∞,-2]∪[2,+∞﹚
D.[-2,0)∪(0,2]
【答案】分析:由题设条件,可得出函数f(x)在(0,2)的函数值为正,在(2,+∞)上的函数值为负,再利用函数奇函数的性质对不等式进行化简,解出不等式的解集,选正确选项
解答:解:∵函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0
∴函数f(x)在(0,2)的函数值为正,在(2,+∞)上的函数值为负
当x>0时,不等式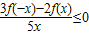 等价于3f(-x)-2f(x)≤0
等价于3f(-x)-2f(x)≤0
又奇函数f(x),所以有f(x)≥0
所以有0<x≤2
同理当x<0时,可解得-2≤x<0
综上,不等式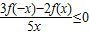 的解集为[-2,0)∪(0,2]
的解集为[-2,0)∪(0,2]
故选D
点评:本题考查函数单调性与奇偶性的综合,解题的关键是综合利用函数的奇偶性与单调性对函数值的符号作出正确判断,对不等式的分类化简也很重要.本题考查了转化的思想及推理判断的能力,有一定的综合性,是高考考查的重点.
解答:解:∵函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0
∴函数f(x)在(0,2)的函数值为正,在(2,+∞)上的函数值为负
当x>0时,不等式
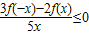 等价于3f(-x)-2f(x)≤0
等价于3f(-x)-2f(x)≤0又奇函数f(x),所以有f(x)≥0
所以有0<x≤2
同理当x<0时,可解得-2≤x<0
综上,不等式
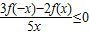 的解集为[-2,0)∪(0,2]
的解集为[-2,0)∪(0,2]故选D
点评:本题考查函数单调性与奇偶性的综合,解题的关键是综合利用函数的奇偶性与单调性对函数值的符号作出正确判断,对不等式的分类化简也很重要.本题考查了转化的思想及推理判断的能力,有一定的综合性,是高考考查的重点.

练习册系列答案
相关题目
设奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时,t的取值范围是( )
| A、-2≤t≤2 | ||||
B、-
| ||||
| C、t≥2或t≤-2或t=0 | ||||
D、t≥
|