题目内容
 (2013•淄博二模)如图,一个类似杨辉三角的数阵,请写出第n(n≥2)行的第2个数为
(2013•淄博二模)如图,一个类似杨辉三角的数阵,请写出第n(n≥2)行的第2个数为n2-2n+3
n2-2n+3
.分析:由三角形数阵看出,从第三行开始起,每一行的第二个数与它前一行的第二个数的差构成以2为公差的等差数列,然后利用累加的办法求得第n行的第二个数.
解答:解:由图看出a(2,2)=3,a(3,2)=6,a(4,2)=11,a(5,2)=18.
由此看出a(3,2)-a(2,2)=3,
a(4,2)-a(3,2)=5,
a(5,2)-a(4,2)=7,
…
a(n,2)-a(n-1,2)=2n-3.
以上n-2个式子相加得:a(n,2)-a(2,2)=3+5+7+…+(2n-3)=
=n2-2n.
所以a(n,2)=n2-2n+3.
故答案为n2-2n+3.
由此看出a(3,2)-a(2,2)=3,
a(4,2)-a(3,2)=5,
a(5,2)-a(4,2)=7,
…
a(n,2)-a(n-1,2)=2n-3.
以上n-2个式子相加得:a(n,2)-a(2,2)=3+5+7+…+(2n-3)=
| (3+2n-3)(n-2) |
| 2 |
所以a(n,2)=n2-2n+3.
故答案为n2-2n+3.
点评:本题考查了类比推理,考查了数列的函数特性,解答此题的关键是找出有效的规律,即从第三行开始起,每一行的第二个数与它前一行的第二个数的差构成以2为公差的等差数列,此题是中档题型.

练习册系列答案
相关题目
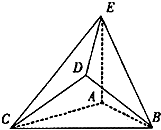 (2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
(2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD. (2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=
(2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=